Mécanique quantique
Groupes de symétrie du modèle standard
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
Dans le modèle standard des particules, les symétries sont reliées à des structures algébriques appelés groupes.

(Figure : vetopsy.fr d'après Geek3)
Symétries exactes
U(1)
$U(1)$ est le groupe de jauge de l’électromagnétisme, théorie de jauge la plus simple constituée par l'électrodynamique classique de Maxwell.
Le groupe $U(1)$ correspond au cercle unité ($T$), composé de tous les nombres complexes ayant comme valeur absolue (ou module) 1 pour la multiplication : $\mathbb T=\{z\in\mathbb C:|z|=1\}$.
La charge électrique $Q$ est conservée, i.e. c'est un nombre quantique conservé de manière additive, i.e. il y a une invariance par transformation de jauge de l'hamiltonien $H$ :
- $|\psi\rangle\rightarrow|\psi'\rangle=e^{-iQ\alpha}|\psi\rangle$ , et donc : $[Q,H]=0$.
-
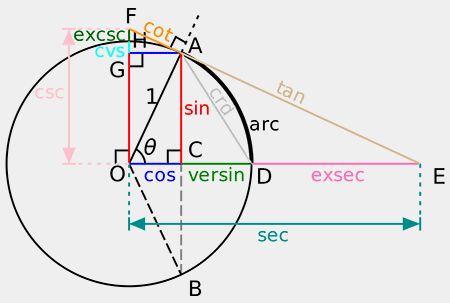
Fonctions trigonométriques
(Figure : vetopsy.fr d'après Steven G. Johnson)

$Q$ est le seul nombre quantique qui correspond au groupe $U(1) global et local.
SU(3)
$SU(3)$ est le groupe associé à l'interaction forte et à la chromodynamique quantique, théorie de jauge des groupes de matrices de Gell-Mann $3\times3$.
Dans, l'algèbre de Lie, il existe des connections entre $SU(2)$ et $SO(3)$, le groupe de rotation en trois dimensions.
Le lagrangien est $\mathcal L_{QCD}=-\dfrac{1}{4}G^a_{\mu\nu}G_a^{\mu\nu}+i\sum\limits_f\bar q^i_f\gamma^\mu(D_\mu)_{ij}q_f^j-\sum\limits_fm_f\bar q^i_fq_{fi}$ où :
- $i$, $j$ et $a$ sont les indices de couleur, $f$ est la saveur du quark, i.e. $u$, $d$, $s$, $c$, $b$ et $t$ ;
-
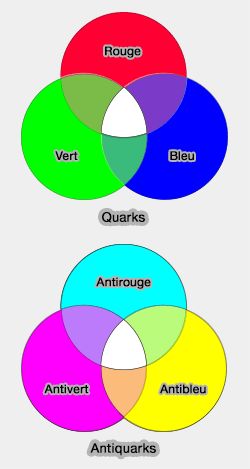
Couleurs des quarks et antiquarks
(Figure : vetopsy.fr) - $q$ est un champ de spineurs de dimension 12, i.e. les trois couleurs multipliées par le quadrivecteur de Dirac ;
- $G_{\mu\nu}^a=\partial_\mu A_\nu^a-\partial_\nu A_\mu^a+g_sf_{abc}A_\mu^bA_\nu^c$ où $f_{abc}$ sont les constantes de structure de $SU(3)$ ;
- $m$ représente la masse des quarks et et $g$, la constante de couplage de l'interaction forte.
Les interactions fortes sont exactement symétriques : on parle de symétrie de couleur.
- Seuls les hadrons sont sensibles à ces interactions entres quarks et gluons, tous deux associés à ce groupe de jauge.
- Le confinement de couleur (ou simplement confinement ou confinement des quarks et des gluons) est une propriété de ces particules élémentaires qui ne peuvent être isolées et sont observées uniquement avec d'autres particules de telle sorte que la combinaison formée soit blanche, c’est-à-dire que sa charge de couleur totale soit nulle. C'est cette propriété qui est à l'origine de l'existence des hadrons.
La généralisation des coefficients de Clebsch-Gordan à $SU(3)$ est utile pour caractériser les désintégrations hadroniques dans la voie octuple qui relie les trois quarks up, down et étrange.
Le groupe $SO(10)$ (cf. unification des forces) est associé à la théorie de grande unification (GUT).
Symétries pouvant être brisées
SU(2)
$SU(2)$ est à la base d'une symétrie " approximative " des trois générations de quarks et de leptons, mais n'est pas un groupe de jauge (théorie des représentations de $SU(2)$)
-
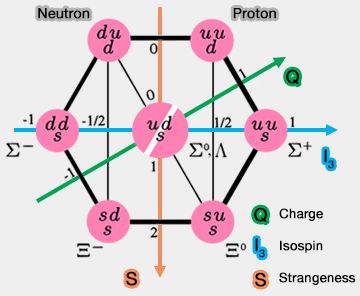
Octet des baryons - Cette symétrie est brisée par les interactions électromagnétiques.
- Toutefois, son utilité réside dans le fait que les ruptures peuvent être décrites par une théorie de perturbation, qui provoque des différences légères entre les états quasi dégénérés.
Cette symétrie est basée sur les matrices de Pauli qui forment, au facteur $i$ près, une base de l'algèbre de Lie du groupe $SU(2)$.
SU(2) x U(1)
$SU(2)$$\;\otimes\;$$U(1)$ est à la base d'une théorie de jauge qui unifie les interactions faibles et électromagnétiques dans l'interaction électrofaible (cf. Le groupe $SU(2)\otimes U(1)$ et la théorie électrofaible).
- Les particules soumises à cette force sont les fermions et les bosons de jauge (photon, bosons Z et W), mais pas les gluons.
-
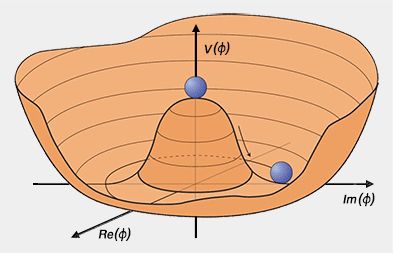
Champ de Higgs
(Figure : vetopsy.fr d'après planetastronomy.com)
SU(3) x SU(2) x U(1)

Le modèle standard de la physique des particules est une théorie quantique des champs de jauge contenant les symétries internes du groupe de produits unitaire $SU(3)\times SU(2)\times U(1)$, considérée comme contenir l'ensemble des particules (quarks, leptons, bosons de jauge et boson de Higgs).
Ce modèle est décrit par les théories de Yang-Mills, après quantification et font appel à la géométrie différentielle et aux espaces fibrés.
- L'invariance locale signifie alors que les équations de Yang-Mills seront inchangées sous l'action de transformations de $G$ sur les champs physiques en chaque point de l'espace-temps.
- Murray Gell-Mann, a prédit l’existence des quarks grâce à la structure des représentations de SU(3).
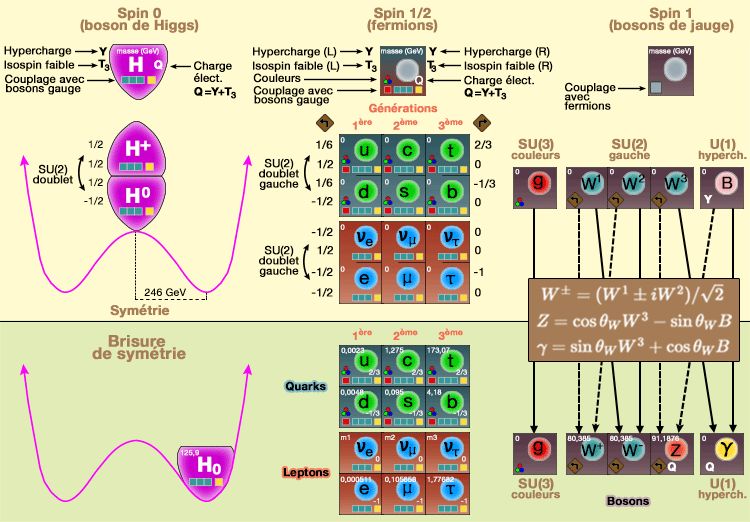
(Figure : vetopsy.fr d'après Latham Boyle)
Remarque : on décrit aussi une supersymétrie où chaque particule a un double supersymétrique (super-partenaires: fermion/boson et boson/fermion dont le spin diffère de 1/2), qui est loin d'être confirmée à l'heure actuelle.
Parité : symétrie P
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétries Groupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


