Mécanique quantique
Moments angulaires : moment angulaire total ($J$)
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires

Dans les deux mécaniques, classique et quantique, le moment angulaire (ou cinétique) est l'une des trois propriétés fondamentales du mouvement avec la quantité de mouvement et l'énergie.
La notion de moment angulaire regroupe plusieurs opérateurs qui ne doivent pas être confondus en mécanique quantique.
- le moment angulaire orbital " classique " ($L$) ;
-
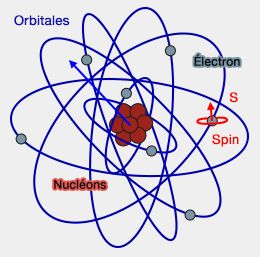
Orbitales et spin
(Figure : vetopsy.fr) - le moment angulaire total ($J$).
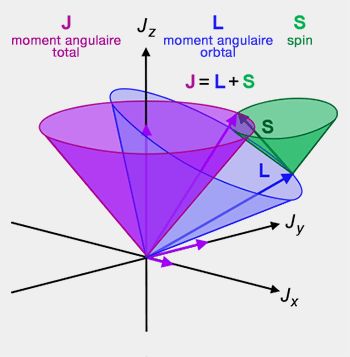
Moment angulaire total
Le moment angulaire total $J$ combine le moment angulaire orbital et le spin par l'équation :
$J=L+S$
Opérateur de moment angulaire total
Comme le moment angulaire orbital $L$ ou le spin $S$, $J$ est représenté, par un opérateur vecteur $J=(J_x,J_y,J_z)$ dont les trois opérateurs ont des relations de commutation identiques à celles de $L$ qui suivent le principe d'incertitude.
- $[J_i,J_j]=i\hbar\sum\limits_{n=1}^{3}\epsilon_{ijk}J_k$, $\forall i,j,k\;\in\{x,y,z\}$,
- où $\epsilon_{ijk}$ représente le symbole de Levi-Civita, i.e. indicateur antisymétrique d'ordre 3 qui peut être exprimé à partir du symbole de Kronecker et ne prendre que trois valeurs : $-1,\;0,+1$.
Le moment angulaire total correspond à l'opérateur de Casimir de l'algèbre de Lie $so(3)$, groupe de rotation $SO(3)$. Les relations d'incertitude du moment angulaire donne comme borne inférieure de l'opérateur de Casimir : $\ell(\ell+1\ge m (m + 1)$ et donc $\ell\ge m$, entre autres.
Par contre, il est possible de mesurer (simultanément) :
- $J^2$, lié au nombre quantique principal (ou interne) de moment angulaire total $j$ par l'équation suivante : $ J^2=\hbar^2j(j+1)$, où $j\in \{0,\;1/2,\;1,\;3/2,\;...\}$, i.e. $|\ell-s|\le j\le \ell +s$ où $\ell$ est le nombre quantique secondaire (ou azimutal) et $s$ le nombre quantique de spin, et $\hbar$ est la constante de Planck réduite ;
Le vecteur de moment angulaire total $j$ est lié au nombre quantique principal de moment angulaire total $j$ par la formule classique $\parallel j\parallel=\sqrt{j(j+1)}\hbar$.
- $J_z$, lié au nombre quantique secondaire de projection du moment angulaire total $m_j$, projection de $J$ sur l'axe quantique classique $z$ : $J_z=\hbar m_j$, où $m_j\in \{-j\;,-(j-1)…\;,+(j-1)\;,+j\}$ : on trouve donc $2j+1$ valeurs pour $m_j$.
Les nombres quantiques $j$ et $m_j$, ainsi que la parité $\mathcal P$, ont tendance à remplacer les trois premiers nombres quantiques $\ell$, $ m_\ell$ et $ m_s$ qui leur sont reliés.
En outre, leurs vecteurs propres sont aussi également des vecteurs propres de l'hamiltonien et des combinaisons linéaires des vecteurs propres de $\ell$, $s$, $m_\ell$ et $m_s$.

$J$ est toujours conservé, ce qui n'est pas le cas de $L$ ou $S$.
Symétrie du moment angulaire total
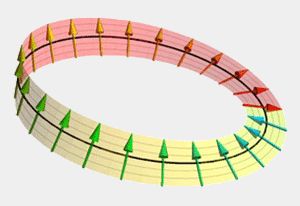
(Figure : vetopsy.fr d'après Slawekb)
La symétrie du groupe est $SU(2)$.
Si le moment angulaire orbital $L$ est de symétrie de groupe de rotation $SO(3)$, le spin $S$ et le moment angulaire total $J$ sont de symétrie $SU(2)$ (cf. connexion entre les deux groupes).
- Si le moment angulaire orbital $L$ provoque une rotation des particules sans modifier le spin, le spin $S$ provoque la rotation du spin sans modifier les positions.
- Le moment angulaire total $J$ fait tourner l'ensemble du système.
Si le moment angulaire total est un demi-entier, la rotation autour de l'axe $z$ par exemple est $R_{otation}(\hat z,360°)=-1$ alors qu'elle est de $+1$ lorsqu'il est entier (
Moments magnétiques
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantique Moments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


