Mécanique quantique
Symétries : quelques définitions

Dans le modèle standard, les trois symétries fondamentales, bien qu'on en trouve des violations, sont représentées par :

• la parité ou symétrie $\mathcal P$,
• l'inversion de charge $\mathcal C$,
• l'inversion du temps $\mathcal T$.

Ces parités sont liées par le théorème $\mathcal C\mathcal P\mathcal T$.

Quelques définitions sur la symétrie

De manière globale on peut retenir que :

L'invariance des équations de mouvement
$\Leftrightarrow$ Opérateur commute avec l'hamiltonien $[O,H]=0$
$\Leftrightarrow$ l'hamiltonien est symétrique
$\Leftrightarrow$ La quantité est conservée.

Symétrie continue/symétrie discrète

La distinction symétrie continue/symétrie discrète renvoie à la structure mathématique du groupe utilisé pour décrire formellement la symétrie.

Reprenons l'opérateur de transformation $U$ et comme il est unitaire, on peut écrire :

$U=e^{i\epsilon A}$, où $A$ est une matrice hermitienne.

Symétrie continue

En mathématiques, la continuité est une propriété topologique d'une fonction.

• La topologie est une branche des mathématiques concernant l'étude des déformations spatiales par des transformations continues (sans arrachages ni recollement des structures).
• En première approche, une fonction f est continue si, à des variations infinitésimales de la variable x, correspondent des variations infinitésimales de la valeur f(x).

• $U=e^{i\epsilon A}\simeq\,$$1+i\epsilon A$,
• l'observable associée à $A$ est conservée : $[S,A]=0$, i.e. $U$ commute avec la matrice-S,
• les valeurs propres sont aussi conservées car $\langle f|[S,A]|i\rangle=0$, et donc $(a_f-a_i)\langle f|S|i\rangle=0$, qui implique que $(a_f-a_i)=0$,
• d'où l'opérateur $A$ est une constante de mouvement.

C'est le cas, par exemple (cf. pavages, rosaces et frises) :

1. des translations (opérateur $D$) :

• dans l'espace : toutes les positions dans l’espace sont physiquement équivalentes, i.e. les propriétés d’un système qui ne subit aucune force externe (système fermé) ne dépendent pas de sa position dans l’espace.

$[D,H]=0\;\Rightarrow[p,H]=0$ et $[p_\mu,H]=0$

• dans le temps : on retrouve la conservation de l'énergie du système ($t\rightarrow t+\Delta t$).

2. des rotations dans l'espace, groupe de rotation $SO(3)$, où les angles de Euler varient de manière continue.

$[R,H]=0\;\Rightarrow[J_z,H]=0$ et comme, un système a symétrie sphérique est invariant par rotation, $[J,H]=0$.

Ces conservations (énergie, quantité de mouvement et moment cinétique) ne sont donc que l’expression, respectivement, de l’homogénéité du temps, de l’espace et l’isotropie de l’espace.

Symétrie discrète

En mathématiques, plus précisément en topologie, la topologie discrète sur un ensemble est une structure d'espace topologique où, de façon intuitive, tous les points sont " isolés " les uns des autres. Les objets étudiés en mathématiques discrètes sont des ensembles dénombrables.

Dans la mécanique quantique, la double action de l'opérateur de transformation laisse le système invariant ce que l'on peut écrire par : $U^2|\psi\rangle$.

• Si $U$ possède des états propres $|\psi_U\rangle$, alors $U|\psi_U\rangle=\eta_U|\psi_U\rangle$, et $U^2|\psi_U\rangle=(\eta_U)^2|\psi_U\rangle=|\psi\rangle$.
• Les valeurs propres $\eta_U$ sont : $\eta_U=\pm1$.
• $U$ est hermitien (ou hermitique) et $\eta_U$ sont les observables.

C'est le cas, par exemple, de la parité (inversion des coordonnées ou symétrie $\mathcal P$), de l'inversion de charge (symétrie $\mathcal C$) ou de l'inversion de temps ((symétrie $\mathcal T$)

Symétrie globale/symétrie locale

La distinction symétrie globale/symétrie locale renvoie à la structure physique de la théorie, en indiquant, si la symétrie dont on parle, peut être appliquée en chaque point de l'espace de façon indépendante ou non.

1. La symétrie est dite globale (ou rigide) si, en l'appliquant à tous les points de l'espace-temps, on arrive à une conformation équivalente.

• Ces symétries nécessitent des lois de conservation, mais pas celle des forces.
• C'est le cas des lagrangiens, utilisés en physique des particules, invariants pour certaines transformations.

Par exemple, l'action du groupe $U(1)$, $U(1)=e^{iq\theta}$, où $\theta$ est une constante sur le lagrangien de Dirac : $\mathcal L_D=\bar\psi(i\gamma^\mu\partial_\mu-m)\psi$ qui transforme la fonction $\psi\rightarrow e^{iq\theta }\psi$ en $\bar\psi\rightarrow e^{-iq\theta}\bar\psi$, et donc $\mathcal L\rightarrow\bar{\mathcal L}=\mathcal L$

2. La symétrie est dite locale si elle agit différemment sur des points de l'espace-temps.

La transformation locale est une transformation de jauge qui transforme le groupe de symétrie en fonction de la variété qui agit différemment selon les points de l'espace-temps : ce peut être une observable, un tenseur or un lagrangien.

• En géométrie, la notion de variété peut être appréhendée intuitivement comme la généralisation de la classification qui établit qu'une courbe est une variété de dimension 1 et une surface est une variété de dimension 2.
• Certaines variétés peuvent être appréhendées par le ruban de Möbius ou la variété de Whitehead.
• Ces symétries sont liées à la chromodynamique quantique ou à l'interaction faible par exemple.

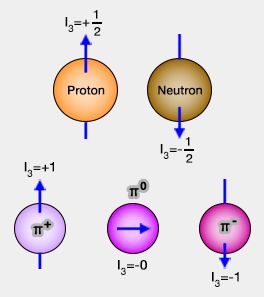
Le proton et le neutron, d'après Werner Heisenberg (1901-1976) sont deux particules qui possèdent une symétrie interne qui permit la découverte de l'isospin : on parle aussi de symétries internes.

Quelques exemples :

• Dans la relativité restreinte, la gravitation est de symétrie globale par exemple en appliquant des rotations et des translations, alors qu'elle est locale dans la relativité générale.
• $SU(2)$ de l'isospin a une symétrie globale.
• Le groupe de symétrie de la supergravité est une symétrie locale, alors que la supersymétrie (SuSY) est une symétrie globale.

Groupes de symétries