Mécanique quantique
Moments magnétiques : moment magnétique orbital

Le moment magnétique est défini comme le vecteur reliant le moment angulaire que subit un objet à l’application d'un champ magnétique externe selon la formule :

$\tau={\mu\wedge B}$

• où $\tau$ est le moment agissant mécaniquement sur le dipôle,
• $B$ le champ magnétique externe et $\mu$ le moment magnétique.

Un moment magnétique ne peut être la conséquence que de deux processus :

• le déplacement de charge électrique,
• le moment magnétique intrinsèque, en relation avec le spin des particules élémentaires.

Ces deux moments magnétiques se conjuguent en un mouvement magnétique total qui a pour conséquence un processus appelé couplage spin-orbite qui est traité dans le chapitre correspondant.

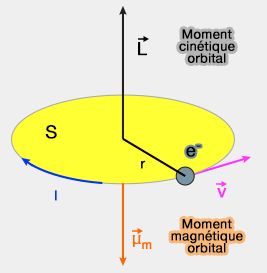
Moment magnétique orbital

Une particule chargée doté d'un moment angulaire $\vec L$, appelé ici moment orbital, crée un champ magnétique $\vec\mu_ m$ (cf. représentation par une boucle de courant).

1. En mécanique classique, le moment magnétique de cette boucle de courant, $\vec\mu_m$, est donné par la formule : $\vec\mu_ m=i\vec S$.

• où $\vec S$ est le vecteur surface associé à la boucle, de direction perpendiculaire au plan du circuit et de module égal à la surface du circuit ;
• $i$ est le courant.

Si la charge de la particule, par exemple l'électron, est $q=-e$ et sa masse est $m$, et qu'il décrit un mouvement circulaire uniforme à la vitesse $v$ sur une orbite de rayon $r$, $T$ est son énergie cinétique, alors :

• $i=\dfrac{-e}{T}$ avec $T=\dfrac{2\pi r}{v}$, d'où $\vec\mu_m=i\vec S=\dfrac{-ev}{2\pi r}\pi r^2=-\dfrac{1}{2}evr$.
• Comme, $\vec\mu_m=-\dfrac{e}{2}\vec r\wedge\vec v$ et que $\vec L=m(\vec r\wedge\vec v)$, alors,
• $\vec\mu_m=-\dfrac{e}{2m}\vec L=\gamma\vec L$ dans laquelle $\gamma=-\dfrac{e}{2m}=\dfrac{q}{2m}$ est appelé rapport gyromagnétique de l'électron.

$\vec\mu_m$ et $\vec L$ ont donc des sens opposés

2. En mécanique quantique, le moment angulaire est quantifié et on sait que $L^2=\hbar^2\ell(\ell+1)$, où $\ell$ est le nombre quantique secondaire (ou azimutal) et $\hbar$, la constante de Planck réduite :

• Comme $\mu=\gamma L$ et que $L=\hbar\sqrt{l(l+1)}$, alors
• $\mu=\left(\dfrac{-e\hbar}{2m}\right)\sqrt{l(l+1)}=\left(\dfrac{-e\hbar}{2m}\right)\sqrt{l(l+1)}$

$\mu_B=\dfrac{e\hbar}{2m}$ est appelé magnéton de Bohr qui est donc le quantum de flux magnétique pour l'électron.

$\mu_B=9,274\;009\;49\;(80)\;10^{-24}\;JT^{-1}$.

3. Si on applique un champ magnétique $\vec B$ à cette particule, son énergie potentielle est augmentée d'un terme :

$V_m=-\vec\mu_m\vec B$

On projette le tout sur l'axe $z$ du sens de l'induction et alors $V_m=-\dfrac{\mu_B}{\hbar}L_z$

• où $L_z=m_\ell\hbar$, projection sur , où $m_\ell$ est le nombre quantique tertaire ou magnétique.
• d'où, $\mu_z=-\mu_Bm_\ell$.

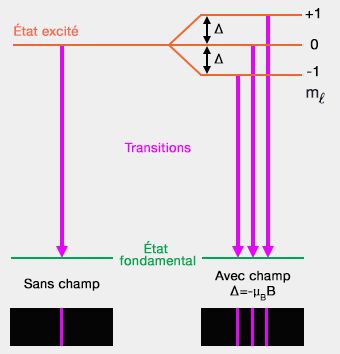
L'hamiltonien du système comporte ce terme supplémentaire $V_m$ et l'énergie de la particule est donc maintenant : $E_{nm}= E_n-\mu_Bm_\ell $.

• Comme $m_{\ell}$ peut prendre différentes valeurs, on observe des écarts énergétiques qui sont à l'origine de l'effet Zeeman.
• Ce processus se nomme levée de dégénérescence par l'induction magnétique, i.e. induit une séparation des niveaux d'énergie dégénérés du système perturbé.

Moment magnétique de spin