Modèle standard des particules
Mésons : pions
- Mécanique quantique
- Modèle standard des particules
- Vue d'ensemble
- Atome
- Fermions
- Bosons
- Réactions nucléaires
- Rayonnements et interactions avec la matière
- Interactions ou forces fondamentales
- Vue d'ensemble
- Comment expliquer que les soient portées par des particules ?
- Que se passe-il en mécanique quantique ?
- Paramètres libres
- Constantes de couplages
- Autres paramètres libres
- Chromodynamique quantique (QCD)
- Électrodynamique quantique (QED)
- Interaction faible
- Interaction électrofaible
- Gravitation
- Modèle de l'univers : Big Bang
Les mésons, bosons (de spin entier), sensibles à l'interaction forte, sont des hadrons,
- composés d'une paire quark/antiquark, donc de taille d'environ 2/3 de celle des nucléons,
-

Les quarks (sans leurs antiparticules)
(Figure : vetopsy.fr)

De nombreux mésons ont été découverts : la liste est consultable avec leurs propriétés.
Pions
Les pions sont impliqués dans la force nucléaire forte pour assurer la cohésion du noyau atomique par l'échange de pions entre les nucléons (neutron et proton).
Vue d'ensemble
Les trois pions $\pi$, sont les mésons les plus légers et, en outre, pseudoscalaires : leur spin est nul.
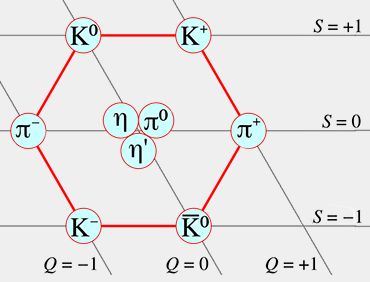
Pions chargés
Les pions chargés sont :
- le $\pi^+$, composé d'un quark $u$ et d'un antiquark $\bar d$ ;
- le $\pi^-$, composé d'un quark $d$ et d'un antiquark $\bar u$ - antiparticule du précédent -.
Ils ont une vie d'environ 2,6 x 10-8 s.
Pion neutre
Le $\pi^0$ est composé d'un mélange $\dfrac{u\bar u-d\bar d}{\sqrt2}$ qui compose un état " vraiment neutre " ($S=0$, $L=0$) avec une conjugaison de charge $\mathcal C$, telle que $\mathcal C=\eta_C^{\pi^0}=-1^{L+S}=1$.
On peut le vérifier par sa désintégration où $\gamma$ est un photon :
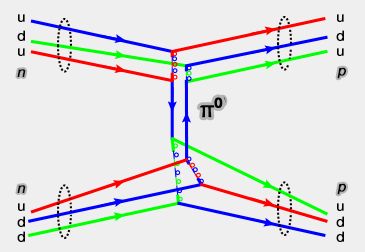
(Figure : vetopsy.fr d'après Fred the Oyster)
$\pi^0\rightarrow\gamma+\gamma$, et donc $\eta_C^{\pi^0}=(\eta_C^{\gamma})^2=1$.
Le $\pi^0$ est sa propre antiparticule et sa vie est courte d'environ 8,4 x 10-17 s.
Interactions entre nucléons :
force nucléaire (force forte résiduelle)
Les nucléons (neutron et proton) n'interagissent pas par l'échange de gluons, car ils ne portent pas de charge de couleur : leurs trois quarks en sont pourvus, mais eux sont blancs.
Cette interaction attractive, appelée force forte résiduelle qui assure la cohésion du noyau, dépend de l'échange de pions et garde ou non la nature des nucléons.
- Si un nucléon échange un pion neutre, $\pi^0$, sa nature est préservée.
- Si un neutron émet un pion $\pi^-$ ou un proton émet un $\pi^+$, ils se transforment en l'autre nucléon.
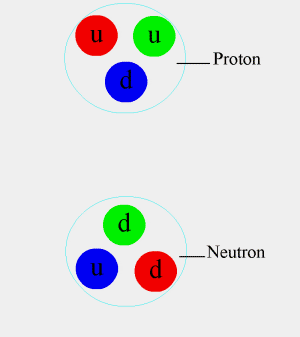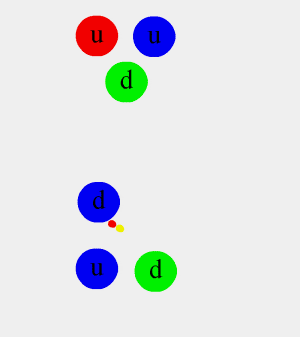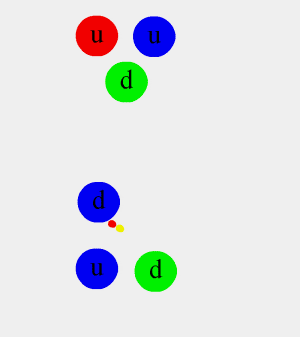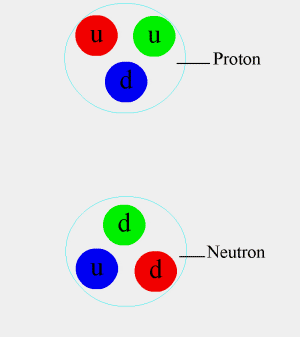
(Figure : Manihearth)
Les pions possèdent un spin nul, leur cinématique dépend de l'équation de Klein-Gordon, version relativiste de l’équation de Schrödinger pour ces particules.
L'interaction entre pions et nucléons est appelée interaction de Yukawa (approche de Hideki Yukawa en 1935).
- La portée des interactions fortes étant d'environ 10−15 m, Yukawa prédit qu'une particule de masse élevée ($m=1/R=100\;MeV$) sans spin devrait être découverte.
- Le muon $\mu$, découvert récemment, ne pouvait convenir car il est insensible aux interactions fortes. Puis en 1947, on découvrit le pion.
- Cependant, cette théorie est trop simpliste et la découverte du boson de Higgs doit inciter à plus de recherches (
 Brisure de symétrie et mécanisme de Higgs p : 25).
Brisure de symétrie et mécanisme de Higgs p : 25).
La symétrie associée est celle de $SU(3)$.
Désintégrations des pions
1. Les pions chargés se désintègrent en :
- $\pi^+\rightarrow\,\mu^++\nu_\mu\;$ et $\;\pi^-\rightarrow\,\mu^-+\bar\nu_\mu$ à 99,98 %,
- $\pi^+\rightarrow\,e^++\nu_e\;$ et $\;\pi^-\rightarrow\,e^-+\bar\nu_e$ à 0,02 %.
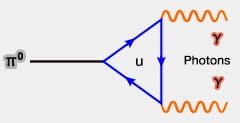
2. Le pion neutre se désintègre en :
- $\pi^0\rightarrow\gamma+\gamma$ dans 98,8 %,
- $\pi^0\rightarrow\gamma+e^++e^-$ dans 0,02 %.
Pions et cosmologie
Les pions sont liés à la limite de Greisen-Zatsepin-Kuzmin (GZK).
L'énergie des rayonnements extrêmes des rayons cosmiques de protons ne devrait pas dépasser cette limite, i.e. on ne devrait pas les observer sur terre.
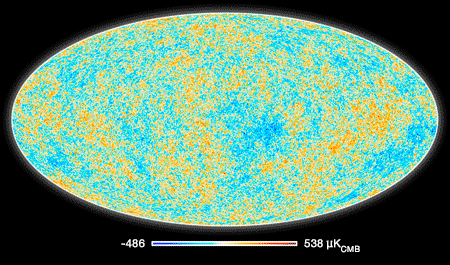
380 000 ans après le Big Bang (Satellite Planck)
(Figure : ESA/collaboration Planck)
Les protons des rayons cosmiques d'une énergie supérieure à 5x1029 eV devraient interagir avec les photons $\gamma_{CMB}$ du fond diffus cosmologique (CMB), et produire des baryons $\Delta$ qui se désintègrent :
- $\gamma_{CMB}+p\rightarrow\Delta^+\rightarrow p+\pi^0$ ,
- $\gamma_{CMB}+p\rightarrow\Delta^+\rightarrow n+\pi^-$.
- $\gamma_{CMB}+p\rightarrow\Delta^+\rightarrow p+e^++e^-$.
Les trois scientifiques ont appelé ce phénomène la coupure GZK ou " GZK-cutoff " en anglais. Or, on observe des rayonnements supérieurs à cette énergie, d'où le paradoxe GZK (ou du rayon cosmique) qu'on ne peut expliquer (cf. rayons cosmiques à énergie extrême).
Leptons
MathématiquesMécanique quantiqueModèle standard des particulesAntiparticulesAtomeNoyauÉlectronsFermionsQuarksBaryonsMésonsLeptonsBosonsGluonsPhotonsBosons W± et Z0Boson de HiggsRéactions nucléairesRayonnements et interactions avec la matièreInteractions fondamentalesInteraction nucléaire forteChromodynamique quantiqueInteraction électromagnétiqueÉlectrodynamique quantiqueInteraction faibleInteraction électrofaibleGravitationAstrophysique et Big Bang


