Mécanique quantique
Couplage spin-orbite
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
Dans le modèle du champ central dans lequel on suppose que chaque électron se déplace indépendamment des autres électrons dans le champ électrostatique, la fonction d'onde d'un électron est appelé spin-orbitale.
- Pour un atome à plusieurs électrons, on définit un hamiltonien du système $H_0$ qui dépend du nombre de charge du noyau.
- Ce modèle donne une bonne approximation des configurations électroniques fondamentales et des énergies d'excitation électronique dans les cas simples.
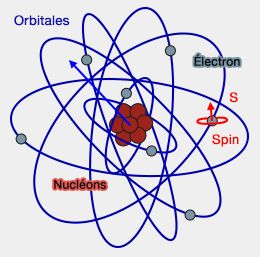
(Figure : vetopsy.fr)
Vue d'ensemble
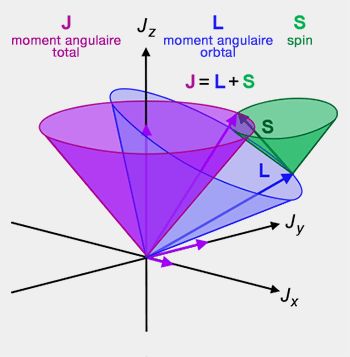
L'interaction spin-orbite (appelée aussi couplage du moment angulaire) est dépendante de la conservation du moment angulaire total $J$.
- Le moment angulaire total $J$ combine le moment angulaire orbital $L$ et le spin $S$ par l'équation : $J=L+S$
- Il faut donc apporter des corrections à l'approximation du modèle du champ central.
L’hamiltonien atomique total est $ H=H_{central}+H_{bi.el.}+H_{SO}$ où :
- $H_{central}$ est l’hamiltonien déterminé par la méthode du champ central,
- $H_{bi.el.}$ est l’interaction biélectronique résiduelle,
- $H_{SO}$ l’interaction spin-orbite.
$H_{bi.el.}=\displaystyle\sum\limits_{i=1}^{N}\left[-\dfrac{Z}{r_i}+\displaystyle\sum\limits_{j<i}^N\dfrac{1}{r_{ij}}\right]-\displaystyle\sum\limits_{i=1}^{N}V(r_i)$ et $H_{SO}=\displaystyle\sum\limits_{i=1}^{N}\xi(r_i)\ell_i\,. s_i$
(Figure : vetopsy.fr)
$H_{bi.el.}$ et $H_{SO}$ sont des hamiltoniens perturbateurs et sont en général assez petits pour pouvoir être traités en développement en perturbation de l’équation de Dirac.
- Par exemple, $\xi(r)$, le potentiel très localisé, augmente en fonction de la lourdeur de l'atome (cf. moment magnétique total).
- $\xi(r)\approx\dfrac{1}{2m^2c^2}\dfrac{1}{r}\dfrac{dV}{dr}$
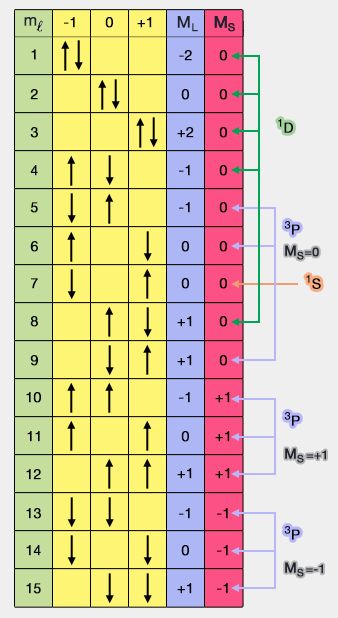
Ces perturbations lèvent la dégénérescence en énergie des états de même configuration, ne différant que par les valeurs de $m_\ell$ (nombre quantique tertiaire ou magnétique) ou de $m_s$, le nombre quantique de la projection du spin sur l'axe $z$.
Grâce aux trois premiers nombres quantiques et en ajoutant $j$, le nombre quantique principal du moment angulaire total et $J_z$, le nombre quantique secondaire de projection de ce moment, on peut calculer l'énergie des micro-états.
Cette interaction spin-orbite est différente :
- pour les électrons selon la lourdeur des atomes
:
- couplage LS, pour les atomes légers, $H_{bi.el.}$ est bien supérieur à $H_{SO}$,
- couplage JJ pour les plus lourds, c'est l'inverse $H_{SO}$ est bien supérieur à $H_{bi.el.}$ ;
- pour le noyau.
Couplage LS
Pour les atomes légers $(Z\le30)$, les interactions électrostatiques entre électrons sont plus fortes que les interactions entre le spin d’un électron et son propre mouvement orbital.
- Chaque micro-état est représenté par le produit de spin-orbitales dont la fonction totale se sépare en un produit d’une fonction d’espace, symétrique pour l’échange, et d’une fonction de spin antisymétrique.
- Toutefois, en l’absence de champ magnétique et d'interaction spin-orbite, tous les états de spin ont la même énergie, i.e. on peut remplacer ces deux fonctions par des combinaisons linéaires normalisées, ici la somme et la différence, ce qui permet de réaliser la séparation espace-spin.
Dans la formule de l'hamiltonien total $H$, on néglige $H_{SO}$.
$ H=H_c+H_{bi.el.}$
Dans ce cas, les moments angulaires orbitaux $\ell_i$, comme les spins de chaque électron $s_i$ s'ajoutent :
$L=\displaystyle\sum\limits_{i=1}^n\ell_i$ et $S=\displaystyle\sum\limits_{i=1}^ns_i$.
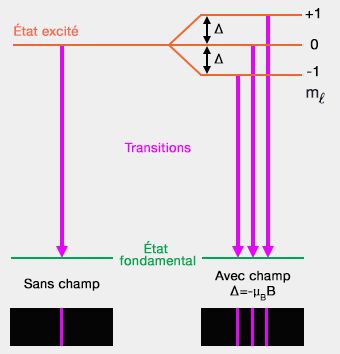
- Cette approximation est seulement valable pour les champs magnétiques très faibles et correspond à l'effet Zeeman (cf. termes spectroscopiques et
Structure atomique et transitions spectrales).
- Cette interaction dédouble certaines raies spectrales pour définir une structure fine.
Sinon, les deux moments L et S se découplent complètement pour donner l'effet Paschen-Back pour les champs forts.
Vous pouvez suivre les calculs dans l'article interaction spin-orbite et dans l'article détaillé 1 et 2.
Couplage JJ
(Figure : vetopsy.fr)
Pour les atomes plus lourds, les interactions spin-orbite des électrons individuels sont plus grandes que celles entre spins ou entre moment angulaires orbitaux (cf. 1.9.2 de Structure des atomes à plusieurs électrons).
- Dans la formule de l'hamiltonien total $H$, on néglige $H_{bi.el}$ : $H=H_c+H_{SO}$
- En effet, $\xi_{n\ell}$ est proportionnel à $Z^4$ (cf. moment magnétique total).
Dans ce cas, chaque électron combine d'abord son spin $s_i$ et son moment orbital $\ell_i$, dans le moment orbital total $j_I$. Dans le couplage JJ, d'où :
$J=\displaystyle\sum\limits_{i}j_i=\sum\limits_{i}(l_i+s_i)$.
Si $H_{bi.el}$ et $H_{SO}$ sont à peu près comparable, le couplage est dit intermédiaire et on doit traiter les deux hamiltoniens isolément.
Couplage nucléaire
Dans les noyaux atomiques, le couplage spin-orbite est beaucoup plus fort que pour les électrons, interaction incorporée directement dans le modèle en couches du noyau atomique.
Toutefois, aucun modèle n'est satisfaisant à l'heure actuelle et les difficultés techniques pour mettre en place des expériences adaptées ne facilitent pas la tâche (cf. chapitre spécial sur la structure du noyau).
Applications du couplage spin-orbite à la configuration électronique
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitales Couplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


