Mécanique quantique
Observables
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
Dans la mécanique classique newtonienne, le vecteur position et la quantité de mouvement décrivent complètement l'état d'un point matériel ($\vec r_M,\vec p_M$).
En d'autres termes, l'état du système, qui décrit tous les aspects de ce système - système dans le sens de partie de l'univers physique choisi pour l'analyse -, permet de déterminer exactement le résultat de mesures qu'on peut y réaliser. Cet état est représenté par un ensemble de grandeurs physiques.
Dans la mécanique quantique, qui est non-déterministe (principe d'incertitude), l'état du système permet seulement de prévoir, de façon toutefois parfaitement reproductible, les probabilités respectives des différents résultats qui peuvent être obtenus à la suite de la réduction du paquet d'onde lors de la mesure.
Observables
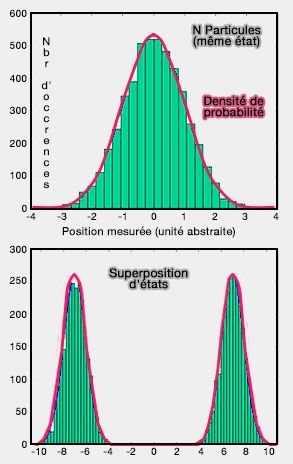
(Figure : v etopsy.fr d'après Perrin)
Vue d'ensemble
Une observable (" beobachtbare Grösse " en allemand disait Wernert Heisenberg : quantité observable) est l'équivalent en mécanique quantique d'une grandeur physique (opérateur mesurable ou jauge) en mécanique classique (position, quantité de mouvement, spin, énergie…).
- Une observable, n'est plus une fonction $f(x,p)$ réelle, mais est un opérateur hermitien $\hat A$ agissant sur un espace de Hilbert $\mathcal H$, et en particulier sur un vecteur de cet espace, chaque vecteur représentant un état quantique.
- L'opérateur $\hat A$ permet de connaître tous les résultats possibles des observables et leur probabilité dans un système quantique donné, c'est-à-dire que cet opérateur pourra décomposer un état quantique quelconque $\vert\psi\rangle$ - un vecteur quelconque de $\mathcal H$ - en une combinaison linéaire d'états propres, chacun étant un état possible résultant des mesures.
Notation bra-ket
La notation bra-ket - en anglais, crochet -, introduite par Paul Dirac (1902-1984) en 1939, montre bien cet aspect vectoriel.
- Un élément quelconque de l’espace des états - espace vectoriel complexe des états appelé $\epsilon$ -, associé disons à la fonction $\psi(r)$, est un vecteur " ket " ou ket tout court : il est noté $\vert\psi\rangle$, appelé $ket\,psi$.
- Il existe un espace dual des états, $\epsilon^\star$, associé aux fonctions complexes conjuguées (qui fait intervenir les conjugués des nombres complexes) des vecteurs de $\epsilon$. Pour tout vecteur ket de $\epsilon$ , correspond un vecteur dual appelé " bra " de $\epsilon^\star$, noté $\langle\phi\vert$, appelé $bra\,psi$.
Quelques propriétés sont essentielles.
Soit $\lambda$, un complexe, $\vert\psi\rangle$ un ket de $\epsilon$.
- $\lambda\vert\psi\rangle$ est aussi un ket : $\vert\lambda\vert\psi\rangle$.
- le bra associé à $\lambda\vert\psi\rangle$ est $\lambda^\star\langle\psi\vert$, $\lambda^\star$ étant le conjugué de $\lambda$, qu'on peut noter $\langle\lambda\psi\vert$.
Le produit scalaire de deux kets $\vert\psi\rangle$ et $\vert\varphi\rangle$ est noté $\langle\psi\;\vert\;\varphi\rangle$.
- $\langle\psi\;\vert\;\varphi\rangle=\langle\varphi\;\vert\;\psi\rangle^\star$
- La loi de Born montre que : $\vert\langle\phi\mid\psi\rangle\vert^2=\vert\langle\psi\mid\phi\rangle\vert^2$.
La normalisation impose que $\langle\psi\;\vert\;\psi\rangle=1$.
L'orthonormalité est donnée par $\langle\psi_i\;\vert\;\psi_j\rangle=\delta_{ij}$, $\delta_{ij}$ étant le symbole de Kronecker.
État quantique

On définit alors l'état quantique comme une distribution de la probabilité associée à chaque observable du système (après la mesure possible sur le système).
- Un mélange d'états quantiques est encore un état quantique appelé mixte.
- Les autres sont appelés états quantiques purs.

1. Mathématiquement, un état quantique pur peut être donc représenté, à un instant t, par un vecteur dans un espace de Hilbert, représenté sous forme d'un ket : $\vert\Psi(t)\rangle$. Toute grandeur physique ($A$) est représentée par un opérateur hermitien ($\hat A$) agissant sur cet espace.
- Soient $\vert α_i\rangle$ les vecteurs propres d'un opérateur $\hat A$, si l'état du système à l'instant de la mesure est un vecteur $\vert\psi\rangle$ de l'espace $\mathcal H$, alors ce vecteur admet la décomposition : $\vert\psi\rangle=\sum\limits{_i}c_i\,\vert\alpha_i\rangle$ où $c_i$ sont des nombres complexes.
- Les états qui s'expriment avant la mesure sous la forme simple $\vert\phi\rangle=c_i\vert\alpha_i\rangle$ sont appelés états propres ou états purs quantiques.
2. L'état quantique mixte d'un système est représenté par la matrice densité $\rho$ (rho) : un état mixte est un mélange statistique d'états purs.
- Cette matrice densité, découverte par John von Neumann (1903-1957) résume en une seule matrice tout l'ensemble possible des états quantiques d'un système physique donné à un instant donné.
- Toutes les propriétés du système (valeurs espérées des observables) peuvent être extraites à partir de cette matrice.

Julius Robert Oppenheimer (1904-1967) devant l'EDVAC
Tout état mixte, peut se mettre sous la forme suivante : $\displaystyle\rho=\sum\limits_{i}p_i|\psi_i\rangle\langle\psi_i|$ où les $\displaystyle p_i$ sont les probabilités du mélange statistique, et les $|\psi_i\rangle\langle\psi_i|$ sont les différents états purs du système.
Les différents mélanges d'états purs génèrent des états équivalents, indistinguables physiquement.
Par exemple, la mesure du spin de l'électron dans une direction quelconque (expérience de Stern-Gerlach), donne deux résultats possibles : up et down. L'espace de Hilbert pour le spin de l'électron est donc en deux dimensions.
- Un état pur ici est représenté par un vecteur complexe à deux dimensions ($\alpha,\beta$), de longueur égale à 1 : $|\alpha|^2|+|\beta|^2=1$, où $|\alpha|$ et $|\beta|$ sont les valeurs absolues de $\alpha$ et $\beta$.
- Un état mixte, dans ce cas, est une matrice hermitienne $2\times2$, positive et de trace $tr(A)=1$.
Avant la mesure (principe d'incertitude), la théorie ne donne qu'une distribution de probabilité pour le résultat pour l'état pur et l'état mixte.
Fonction d'onde
La représentation d'un état quantique peut être décrit par une fonction mathématique appelée fonction d'onde, $\left\vert\Psi(t)\right\rangle$, donné en respectant les contraintes imposées par les relations d'Heisenberg (principe d'incertitude).
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitude Observables État quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


