Mécanique quantique
Moments magnétiques : moment magnétique total
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
Les deux moments magnétiques (orbital et spin) des particules se conjuguent en un mouvement magnétique total qui a pour conséquence un processus appelé couplage spin-orbite qui est traité dans le chapitre correspondant.
Moment magnétique total
Ce couplage produit une énergie potentielle, dans un système hydrogénoïde - cation ne possédant qu'un seul électron - à charge nucléaire $Ze$ (cours de magnétisme) :
$V=\dfrac{Ze^2}{8\pi\epsilon_0m^2_ec^2r^3}\vec L\;.\vec S$
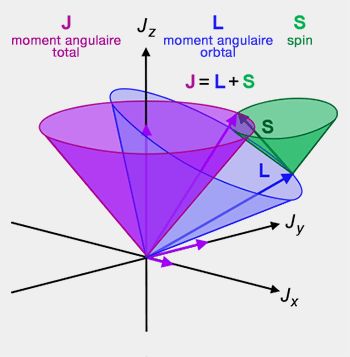
Comme le moment angulaire total est $\vec J=\vec L+\vec S$, on en déduit que :
$J^2= L^2+S^2+2L\;.S$, d'où $L\;.S=\dfrac{1}{2}(J^2-L^2-S^2)$.
Les éléments de la base propre des cinq opérateurs $H$, $J^2$, $L^2$, $S^2$ et $J_z$, sont les cinq nombres quantiques :
- $n$ (nombre quantique principal),
- $j$ (nombre quantique du moment angulaire total),
- $\ell$ (nombre quantique du moment angulaire orbital),
- $s$ (nombre quantique de spin)
- $J_z$ (la composante z du moment angulaire total).
Cette énergie potentielle, où $ a_0$ est le rayon de Bohr, dépend de :
$\left\langle\dfrac{1}{r^3}\right\rangle=\dfrac{2Z}{a_0^3n^3(\ell+1)(2\ell+1)}$ et de $\langle L\;.S\rangle=\dfrac {\hbar^2}{2}(J(J+1)-L(L+1)-S(S+1)$
La levée de dégénérescence d'un niveau caractérisé par les nombres quantiques principal $n$ et le nombre quantique secondaire (ou azimutal $\ell$) est caractérisé par :
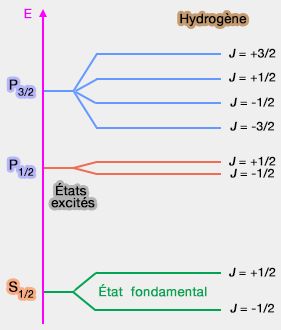
(Figure : vetopsy.fr)
$\xi_{n\ell}=\dfrac{Ze^2}{8\pi\epsilon_0m^2_ec^2}\left(\dfrac{Z}{a_0}\right)^3\dfrac{1}{n^3\ell\left(\ell+\dfrac{1}{2}\right)(\ell+1)}$
Pour tout atome mono-ionisé à Z protons :
$\xi_{n\ell}=Z^4\dfrac{\mu_0}{4\pi}g_s\mu^2_B\dfrac{1}{n^3a_0^3\ell\left(\ell+\dfrac{1}{2}\right)(\ell+1)}$
- où $g_s$ est le facteur de Landé de l'électron,
- $\mu_B$, le magnéton de Bohr.
Vous pouvez suivre les calculs dans l'article interaction spin-orbite et dans l'article détaillé 1 et 2.
Dans les cas où $ Z$ est faible, on peut négliger ce couplage spin-orbite. Mais, comme $\xi_{n\ell}$ est proportionnel à $Z^4$, il faut en tenir comme sur des atomes lourds d'où le couplage comme appelle JJ.
Soit un niveau $^2P$, ce couplage spin-orbite décompose les classiques :
- $^2P_{1/2}$ en 2 raies avec $j=-1/2,\;+1/2$ ;
- $^2P_{3/2}$ en 4 raies avec $j=-3/2,\;-1/2,\;+1/2,\;+3/2$.
- Les facteurs de Landé sont différents respectivement, 2/3, 4/3 et 2 pour $S_{1/2}$, ce qui, explique les différences de niveau énergétique.
Spin-orbitales et micro-états
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulaires Moments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


