Mécanique quantique
Groupes de symétrie : vue d'ensemble
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
Dans le modèle standard des particules, les symétries sont reliées à des structures algébriques appelés groupes, et en particulier les groupes de Lie.
Groupe spécial unitaire SU(n)

Le groupe spécial unitaire $SU(n)$ de degré $n$ est un groupe de Lie de matrices unitaires $n\times n$ de déterminant 1 $(det(I)=1)$.
- L'opération de groupe est celui de la multiplication matricielle qui préserve le produit scalaire sur $\mathbb C^n$ (groupe classique compact).
- Le groupe spécial unitaire est un sous-groupe du groupe unitaire $U(n)$ - $SU(n)\subset U(n)\subset GL(n,\mathbb C)$ -.
L'algèbre de Lie, du nom de Sophus Lie (1842-1899), correspondant aux groupes de Lie $G$, est notée $\mathfrak g$. Ces espaces vectoriels sont dotés d'une loi de composition interne bilinéaire, antisymétrique et qui vérifie la relation de Jacobi.
- Ces groupes de Lie définissent en particulier la symétrie continue en mathématiques et en physique théorique (par exemple la théorie des quarks).
- On peut voir des exemples de groupes de Lie sur l'article de Wikipedia.
La description du groupe spécial unitaire $SU(n)$ montre que l'espace vectoriel est muni de l'algèbre $\mathfrak su(n)$.
Il s’agit de l’algèbre des matrices complexes $n\times n$ antihermitiennes : $A^\dagger=-A$, i.e., le conjugué transposé est égale à son opposé.
La multiplication matricielle définit le produit $[x,y]$ appelé " crochet de Lie ".
- $[x,y]=xy-yx$ définit le commutateur d'où on déduit que :
-

Hermann Weyl (1885-1955)
En physique des particules, on multiplie le commutateur par -i.
La relation (ou identité) de Jacobi, du mathématicien allemand Carl Gustav Jacob Jacobi (1804–1851), est exprimée par :
- $[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0$.
- C'est la condition nécessaire pour qu'un espace vectoriel $V$, muni d'une application bilinéaire antisymétrique $\left[\cdot,\cdot\right]$ soit un crochet de Lie, i.e $\forall x,y\in V$, alors $[x,y]\in V$.
Les matrices sont de trace nulle - $tr(A)=0$ - et de déterminant 1 - $det(A)=1$ -.
$\mathfrak su(n)$ a une dimension (ou variété) de $n^2-1$.
Groupes de jauge
En théorie quantique des champs, les groupes de jauge $(G)$ sont des groupes de symétrie locale dont les éléments ne changent pas la valeur du lagrangien du système étudié lorsqu'ils s'appliquent au champ qui figure dans le lagrangien : on parle d'invariance de jauge (Hermann Weyl - 1918 -).
Cette notion est à la base de la théorie de jauge et à la transformation de jauge qui est la transformation unitaire :
- $\psi\rightarrow\psi'=e^{-ie\alpha}\psi$
-
où $e$ est un paramètre constant et $\alpha(x)$ une fonction arbitraire.
-
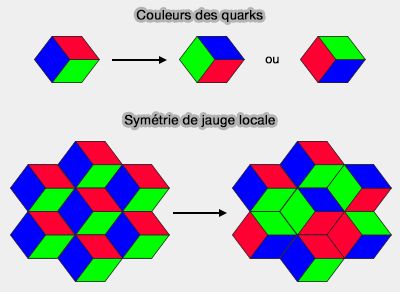
Couleurs des quarks et symétrie de jauge locale
(Figure : vetopsy.fr d'après Fabien Besnard) - Si $\alpha(x)$ est une fonction scalaire dépendante de la position, la transformation de jauge est dite locale.
-
L’invariance d’un système par rapport à une transformation de jauge locale est essentielle pour la description du modèle standard de la physique des particules. Les groupes agissant dans cette théorie sont (théorie de jauge. Modèle standard) :
- le groupe unitaire $U(1)$ pour le champ électromagnétique, i.e. théorie de jauge la plus simple constituée par l'électrodynamique classique de Maxwell. $SU(n)$ est un sous-groupe de $U(n)$.
- les groupes spéciaux unitaires SU(3) pour la chromodynamique quantique,
- SU(2)xU(1) pour l'interaction électrofaible,
- SU(3)xSU(2)xU(1) pour le modèle standard.
Symétries exactes et approximatives
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétries Groupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


