Nombres quantiques
Vue d'ensemble
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires

Les nombres quantiques décrivent les valeurs de quantités conservées dans la dynamique d'un système quantique.
Dans la mécanique quantique, comme son nom l'indique, on observe une quantification des observables : ce sont des nombres entiers ou demi-entiers, i.e. formant des ensembles discrets qui caractérisent un état quantique.
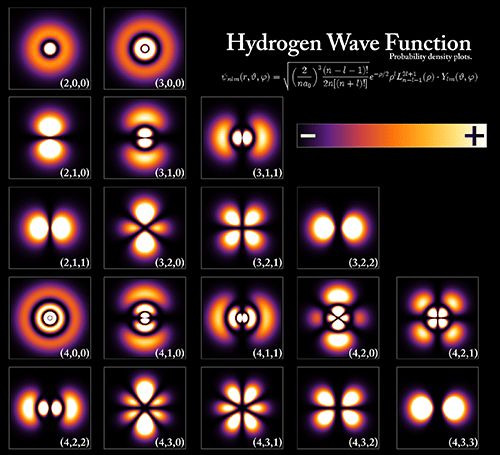
Une analyse complète d'un système quantique fait intervenir les nombres quantiques pour décrire son hamiltonien (énergie totale) qui est aussi un nombre quantique.
- Chaque nombre quantique commute avec cet hamiltonien (théorème de Noether).
- On doit choisir des opérateurs ($\hat Oper$) qui peuvent varier suivant les situations.
En général, quand on parle des nombres quantiques,
- on pense aux nombres quantiques des moments angulaires et magnétiques, mais,
- il en existe d'autres.
Nombres quantiques
dits " intrinsèques "
En mécanique classique, on pensait qu'un électron tournait autour du noyau sur des orbites circulaires, un peu comme une planète autour du soleil. Une particule était alors caractérisée par six paramètres : les trois paramètres de position (x, y, z) et les trois paramètres de vitesses (vx, vy, vz).
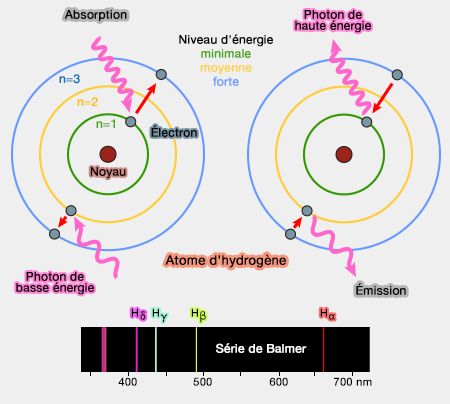
(Figure: vetopsy.fr)
En mécanique quantique, dans le modèle de l'atome de Bohr, l'électron peut être entièrement défini par un jeu de quatre nombres quantiques, nommé case quantique.
Les cases quantiques sont les places dans les orbitales atomiques qui peuvent être occupées par un électron, ou par une paire d'électrons de spin complémentaires : ce sont des portions de l'espace (volume) dans lesquels il y a une grande probabilité de trouver l'électron.
Les nombres quantiques dits " intrinsèques " spécifient cette case quantique.
Les trois premiers permettent de décrire les orbitales :
- le nombre quantique principal - $n$ -, qui définit la taille et l'énergie de l'orbitale,
- le nombre quantique secondaire (ou azimutal) - $\ell$ -, qui définit la forme de l'orbitale (moment angulaire orbital),
- le nombre quantique tertiaire ou magnétique - $m_\ell$ -, qui définit l'orientation de l'orbitale dans l’espace (projection du moment angulaire orbital).
Les trois premiers nombres quantiques sont des solutions de l’équation de Schrödinger. La fonction d'onde exprimée en coordonnées sphériques peut être décomposée en un produit de trois fonctions.
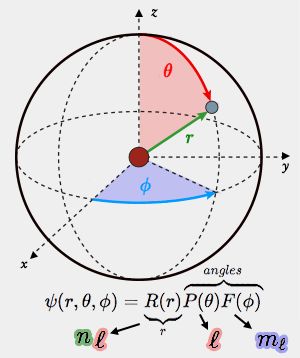
(Figure : vetopsy.fr)
$$\psi(r,\theta,\phi)=\underbrace{R(r)}_{n,l}\overbrace{P(\theta)F(\phi)}^{\ell,\;m_\ell}=R_{n,l}(r)Y_{\ell, m_\ell}(\theta,\phi)$$
Comprendre de manière didactique la relation entre l'équation de Schrödinger et les trois premiers nombres quantiques (hyperphysique : l'atome d'hydrogène).
Le quatrième est le nombre quantique de spin - $s$ -, spin qui est le moment angulaire intrinsèque des particules, essentiel en mécanique quantique, qui n'a pas d'équivalent en mécanique classique.
L'équation de Dirac, en 1928, a pris en compte le spin dans le contexte de la relativité restreinte.

Ces quatre nombres définissent les spin-orbitales.
Selon le principe d'exclusion de Pauli pour les fermions, deux électrons appartenant à un même atome ne peuvent avoir leurs quatre nombres quantiques identiques.
Les études spectroscopiques ont montré qu'il existait une structure fine et une structure hyperfine qui fait intervenir une série discrète de nombres liés à des valeurs demi-entières. C'est le cas
- du moment angulaire ou cinétique total du système $J$,
- du couplage des spins des électrons et du noyau $F$.
Autres nombres quantiques

Toutefois, d'autres nombres quantiques définissent :
- des valeurs atomiques comme le nombre baryonique $B$, le nombre leptonique total $L$ ou le nombre quantique hypothétique de charge $X$ ;
- des nombres quantiques de saveurs :
- les nombres leptoniques spéciaux : $L_{\displaystyle e}$, $L_{\displaystyle\mu}$, $L_{\displaystyle\tau}$ ;
- les nombres quantiques de saveur des quarks, strangeness $S$, charm $C$, bottomness ou beauty $B'$ ou $\tilde B$ et topness $T$ ;
- les charges de couleur des quarks (rouge, vert, bleu) ;
- la charge électrique $Q$ ;
- l'isospin $I_3$ et l'hypercharge $Y$ ;
- l'isospin faible $T_3$ l'hypercharge faible $Y^W$ ;
- la parité $\mathcal P$.
Nombre quantique principal
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiques Nombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


