Mécanique quantique
Moments angulaires : applications du spin

Le spin est le moment angulaire ou cinétique intrinsèque des particules quantiques : il définit l'orientation des particules dans un champ magnétique.

La découverte du spin a révolutionné plusieurs domaines.

Modèle standard des particules élémentaires

Grâce au spin, le modèle standard des particules élémentaires a pu être précisé.

Les couplages spin-orbite permettent d'expliquer :

• le remplissage successif des couches électroniques selon les niveaux d'énergie des électrons et le principe d'exclusion de Pauli ;
• les décalages dans les niveaux d'énergie des électrons que l'on observe dans la séparation des raies spectrales, ce que l'on appelle la structure fine ;
• la description du modèle en couches du noyau atomique, i.e. phénomène identique au précédent, mais cette fois-ci dans le noyau, c'est-à-dire au niveau des nucléons ;
• les décalages dans la résonance orbitale en astronomie.

En 1928, Paul Dirac (1902-1984) introduit le spin, découvert par l'expérience de Stern et Gerlach en 1922, dans l’équation de Schrödinger.

Les solutions de l'équation de Dirac, équation relativiste, prédisent aussi l'existence des antiparticules.

Spintronique

La spintronique, à la limite entre l'électronique et du magnétisme, dans les années 1980, a permis de développer des nouvelles techniques, en utilisant le spin de l'électron, en plus de sa charge électrique, comme dans l'électronique traditionnelle.

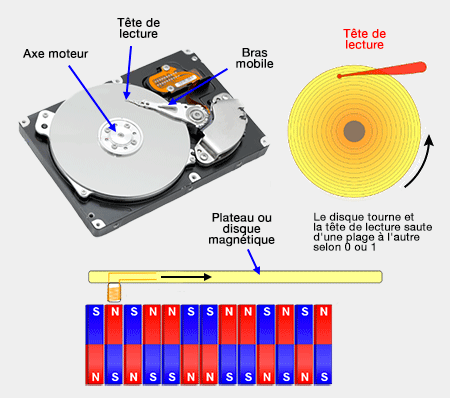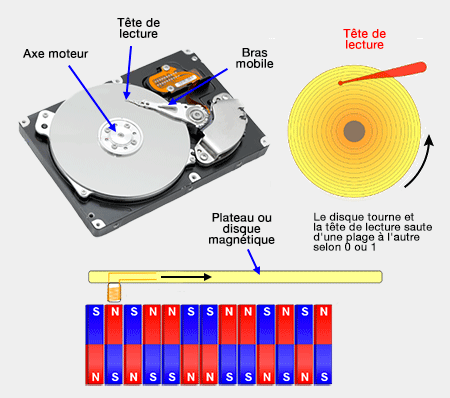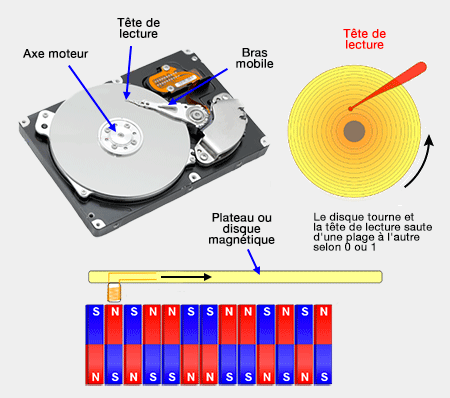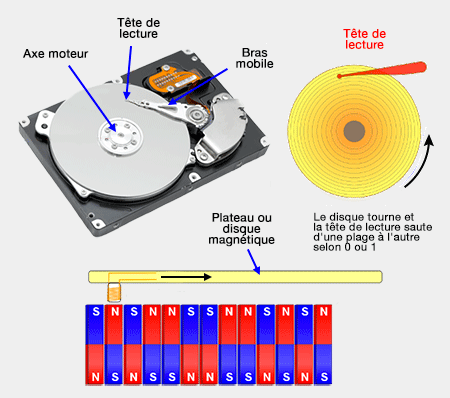
La magnétorésistance géante (GMR) est employée, par exemple dans le stockage des données sur un disque dur de plus en plus miniaturisé d'un ordinateur (cf. petit manège : le spin des électrons).

C'est un effet quantique provoqué par le comportement du spin de l'électron dans les structures de films minces composées d'une alternance de couches ferromagnétiques et de couches non-magnétiques communément appelées multicouches.

En 1930, Nevill Mott (1905-1996) découvrit que des impuretés dans des métaux aimantés (fer, nickel, cobalt), freinaient de manière différente les élections de spin up et down. C'est Albert Fert et Peter Grünberg, colauréats du prix Nobel de physique 2007, qui découvrirent, de manière indépendante, la GMR en 1988, grâce à une nouvelle technique appelée épitaxie par jets moléculaires qui permet la fabrication de multicouches magnétiques de 1 nm environ (couche mince). L'épitaxie est une croissance orientée.

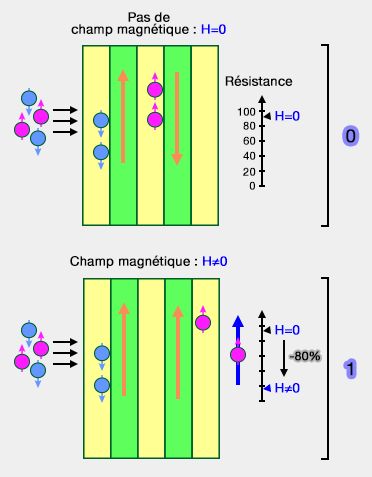
Au départ, on a utilisé des multicouches alternées d'un métal magnétique, le fer, et non-magnétique, le chrome, de 3 couches d'atomes : les couches de fer s'orientent naturellement de manière antiparallèle, leur aimantation est de sens opposé, d'où un champ électromagnétique nul ($H = 0$).

Si l'on se représente deux couches de fer (cf. figure) : la première des couches arrête les électrons de spin down et l'autre, les électrons de spin up : la résistance électrique est très forte, proche de 100%.

Si on applique maintenant un champ magnétique à cette multicouche, les aimantations des deux couches de fer s'alignent dans la direction du champ : les électrons dont le spin est dans la même direction passent (alors que ceux de direction opposée restent bloqués), ce qui a pour conséquence de diminuer fortement la résistance (de 80% environ), d'où le nom donné à ce phénomène : magnétorésistance géante (GMR).

Supposons que, sur une première couche, le champ magnétique reste toujours orienté dans la même direction, les électrons de spin correspondant passent. Sur la deuxième couche, si on applique un champ magnétique :

• de direction opposé, les électrons sont arrêtés, le courant ne passe plus et $H=0$.
• de même direction, les électrons continueront à passer et H est non nul, on définit $H=1$.

On retrouve les 0 et 1 générés par les impulsions électromagnétiques sur le disque dur, dont les couches de plus en plus fines sont lues par une tête de lecture ultrasensible basée sur la GMR.

Résonance magnétique

Le spin non nul est utilisé dans les phénomènes de résonance quand les particules sont soumises à un champ magnétique.

Un spin non nul est ainsi toujours associée à un moment magnétique non nul ($\mu$) par la relation $\mu = \gamma S$, où $\gamma$ est le rapport gyromagnétique, qui intervient dans les phénomènes de résonance magnétique.

1. La résonance magnétique nucléaire (RMN) s'applique aux noyaux.

• Lorsqu'ils sont soumis à un rayonnement électromagnétique, les noyaux atomiques à spin non nul absorbent l'énergie, puis la restituent lors de la relaxation.
• Cette énergie correspond à une fréquence très précise, dépendant du champ magnétique et d'autres facteurs moléculaires.
• Ce phénomène permet donc l'observation des propriétés quantiques magnétiques des noyaux dans les phases gazeuses, liquides ou solides.

Ce processus permet de fournir des informations détaillées sur la structure et la conformation des molécules.

L'IRM, imagerie par résonance magnétique, est utilisée en médecine par exemple (cf. spectroscopie de résonance magnétique nucléaire).

2. La résonance de spin électronique (ESR) ou résonance paramagnétique électronique (RPE) s'applique aux électrons (non appariés).

La résonance quadripolaire nucléaire (RQN) est un phénomène proche, mais en l'absence de champ magnétique (zero Field NMR ou RMN en champ nul), pour des noyaux à spin ≧ 1 dits " quadripolaires ", car contrairement aux particules de spin 1/2 " dipolaire ", ils possèdent en plus un moment électrique quadripolaire.