Principe de relativité
Relativité restreinte : simultanéité (exemple du train)
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires
La relativité restreinte (" special relativity en anglais ") est basée sur le troisième article de juin 1905 (" De l'électrodynamique des corps en mouvement ") implique deux postulats.
1. Le principe de la relativité : « Toutes les lois de la physique doivent être les mêmes pour tous les observateurs se déplaçant à vitesse constante les uns par rapport aux autres. En conséquence, elles auront la même forme mathématique pour tous ces observateurs. Cela équivaut à reconnaître l'impossibilité de détecter le mouvement uniforme absolu. »

2. « La vitesse de la lumière dans le vide est la même pour tous les observateurs inertiels. » La vitesse de la lumière une constante fondamentale de la physique : $c=299\,792\,458\;m\cdot s^{-1}$.
- Cette invariance de la vitesse est incompatible avec la mécanique classique newtonienne.
- Einstein reprend ici la théorie de Maxwell, dans laquelle la vitesse de la lumière est finie, mais qui comporte un référentiel privilégié, l'éther.
Se pose alors le problème de la simultanéité, i.e. le fait que deux événements se produisent au même moment.
Problème de la simultanéité
Einstein prend l'exemple du train dans son article : « si nous disons " qu'un train arrive ici à 7 heures ", cela signifie " que la petite aiguille de ma montre qui pointe exactement le 7 et que l'arrivée du train sont des évènements simultanés ". Il peut sembler que toutes les difficultés provenant de la définition du « temps » peuvent être supprimées quand, au " temps ", nous substituons " la position de la petite aiguille de ma montre ". Une telle définition est dans les faits suffisante, quand il est requis de définir le temps exclusivement à l'endroit où l'horloge se trouve. Mais elle ne suffit plus lorsqu'il s'agit de relier chronologiquement des évènements qui ont lieu à des endroits différents - ou ce qui revient au même - d'estimer chronologiquement l'occurrence d'évènements qui surviennent à des endroits éloignés de l'horloge. »
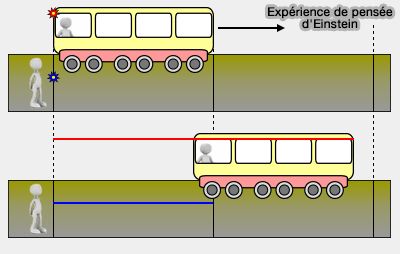
(Figure : vetopsy.fr)
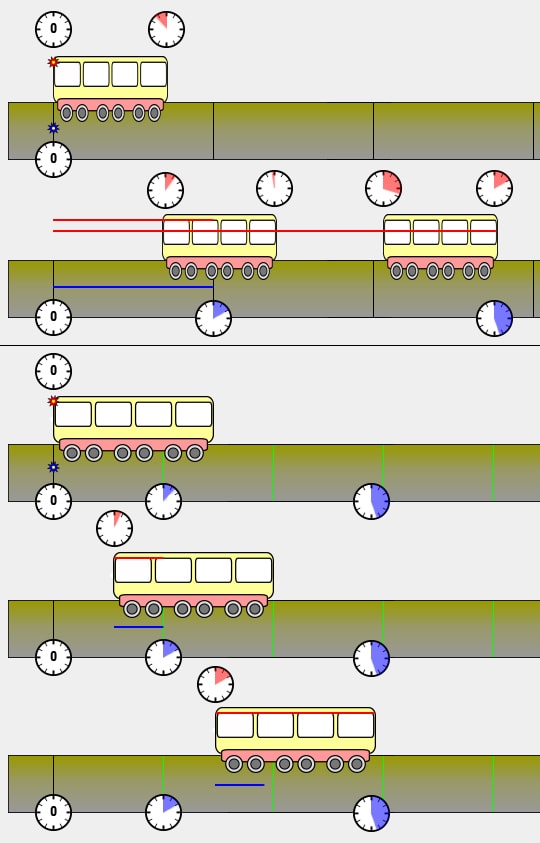
Prenons l'exemple bien connu du train qui voyage à très grande vitesse (constante) avec un passager à l'arrière du train et un observateur immobile sur le quai. Quand les deux personnes se retrouvent exactement au même niveau (pointillé sur la figure), chacun allume un laser pointé dans la même direction.
- La vitesse de la lumière étant constante, les deux faisceaux (rouge et bleu) arrivent en même temps à l'avant du wagon (application de 1).
- Le passager dira que le faisceau laser (la lumière) s'est déplacé d'une longueur de wagon.
- L'observateur dira que la lumière s'est déplacée de la longueur du wagon + la distance parcourue par le wagon, ce qui est impossible.
Quand on parle de vitesse constante, on parle de longueur divisée par une durée, ce quotient devant être constant du point de vue de l'observateur et du passager.
(Figure : vetopsy.fr)

Comment expliquer cela ?
Hypothèses
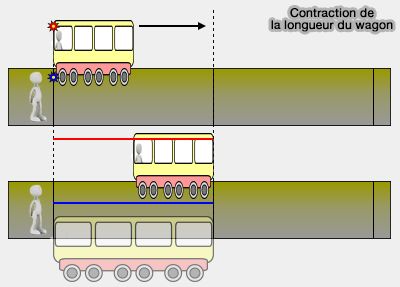
1. Première hypothèse : si les résultats sont identiques du point de vue du passager et de l'observateur, i.e. le faisceau laser s'est déplacé d'une longueur de wagon - le wagon n'étant pas immobile, ce qui serait une solution - cela veut dire que :
- pour l'observateur, la longueur du wagon perçue est plus petite ;
- pour le passager, la longueur du train reste identique.

On parle de contraction des longueurs.
Mais attention, c'est uniquement un problème un point de vue : si on voit quelqu'un de loin, il paraît plus petit que s'il est plus proche. Pourtant, on sait qu'il garde la même taille, mais c'est la mesure que l'on en fait, i.e. angle sous lequel on le voit - qui change: on parle alors de distance angulaire.
(Figure : vetopsy.fr)
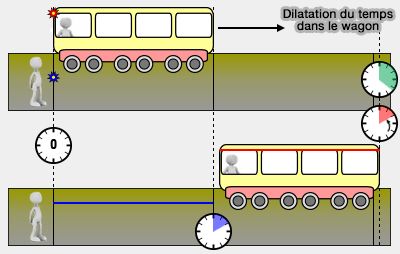
2. Deuxième hypothèse : si les résultats ne sont pas identiques, i.e. la longueur sur le quai est supérieure à celle du wagon, c'est le temps écoulé qui n'est plus identique.
- Le trajet mesuré dans le train est plus court que celui mesuré sur le quai.
Conséquence étonnante : le passager est donc plus jeune que l'observateur !
- Le temps doit s'écouler plus lentement sur le quai que dans le train pour garder la vitesse constante.

On parle de dilatation du temps.
(Figure : vetopsy.fr)
3. Tout cela paraît cohérent, mais il faut maintenant vérifier que l'inverse est vrai à cause du postulat d'équivalence des référentiels inertiels : ces propriétés doivent être symétriques.
- ou le quai est plus court : c'est lui qui se contacte car il est en mouvement par rapport au wagon immobile. La lumière arrive trop vite, i.e. elle plus rapide que la vitesse de la lumière.
- ou le temps se dilate sur le quai par rapport au wagon : la distance est alors trop courte.

On voit bien que cela ne marche pas.
Introduction de
l'inclinaison du temps
Comment essayer de comprendre ces phénomènes ?
et inclinaison du temps
(Figure : vetopsy.fr)
Pour comprendre un peu plus facilement :
la relativité restreinte expliquée en animation,
-
la relativité restreinte 2/2 de e-penser,
- introduction à la relativité restreinte.
Pour mieux appréhender ces concepts, cf. la page sur les diagrammes de Minkowski.
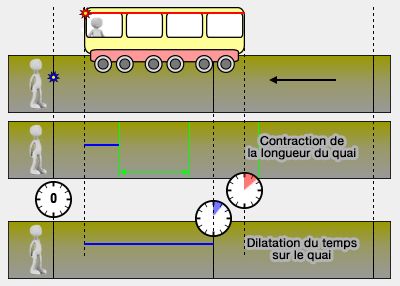
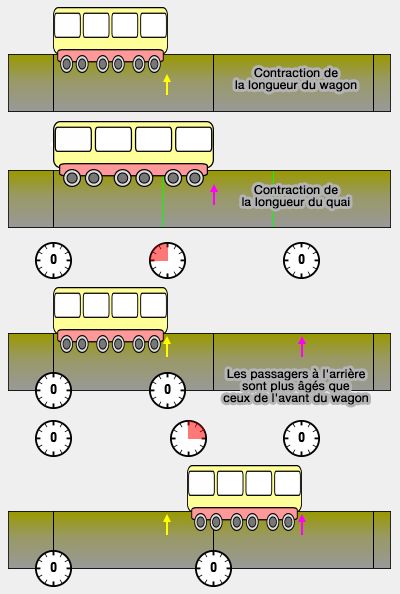
1. La symétrie des contractions des longueurs nous pose un problème car, comment se fait-il que le wagon soit plus petit et le quai puisse l'être aussi ?
- Du point de vue de l'observateur, quand le wagon est contracté, on marque une flèche jaune qui indique l'avant du wagon.
- Du point de vue du passager, quand le quai est contracté, on marque une flèche violette sur le quai qui indique l'avant du wagon.
2. Si on reprend le point de vue de l'observateur, il voit alors deux marques distinctes sur le quai, vu que le quai a repris sa taille " normale ".
3. Quand la simultanéité est présente à l'arrière du wagon, elle ne l'est plus à l'avant, i.e. il y a donc plus de simultanéité entre l'arrière et l'avant du wagon.
Du point de vue de l'observateur, il est minuit à l'arrière et à l'avant du wagon (flèche jaune).
Du point de vue du passager, il est aussi minuit à l'avant du wagon (flèche violette).
- Or, il faut bien un laps de temps pour parcourir le trajet entre la flèche jaune et la flèche violette, cela veut dire qu'il n'était pas encore minuit à la flèche jaune.
- Plus on s'éloigne de la flèche voilette plus le temps est grand : il faut donc se servir d'un gradient de vitesse.
- Il est minuit à arrière du wagon, mais pas encore à l'avant du wagon (flèche jaune) (disons, $-15$ secondes) : le temps n'est pas unique, mais s'incline vers le passé.
(Figure : vetopsy.fr)
Quand le wagon avance, l'intervalle de temps est conservé, i.e. il sera minuit à la flèche violette à l'avant du train, mais $+15$ secondes à l'arrière du train pour garder la symétrie.

Les passagers à l'arrière seront plus âgés que les passagers à l'avant pour l'observateur !
L'inclinaison du temps permet de garder cette symétrie.
Expérience
complète

En fait de compte, les trois phénomènes, contraction des longueurs, dilatation du temps et inclinaison du temps, se combinent pour conserver les phénomènes symétriques dans tous les référentiels.
Quand le rayon laser arrive à l'avant du wagon, les temps dans le wagon et sur le quai sont identiques (cf. figure 5).
La différence de temps entre l'arrière et l'avant n'est qu'un effet de perspective, comme pour la taille des personnes auparavant.
On voit que la situation symétrique marche aussi !
Explications
mathématiques
Vous pouvez aller sur l'article " introduction à la relativité restreinte " pour voir les équations.
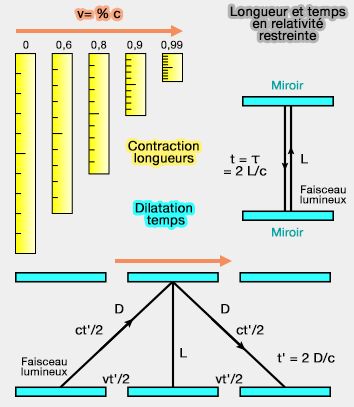
Pour passer d'un référentiel à l'autre, on utilise une transformation de Lorentz avec (cf. calculs) :
- $x'=\dfrac{x-vt}{\sqrt{1-{\frac{\nu^2}{c^2}}}}$, $y'=y$, $z'=z\quad$ et $\quad t'=\dfrac{t-\dfrac{v}{c^2}x}{\sqrt{1-{\frac{\nu^2}{c^2}}}}$.
(Figure : vetopsy.fr)
Le facteur de Lorentz est : $\gamma=\dfrac{1}{\sqrt{1-{\frac{\nu^2}{c^2}}}}=\dfrac{1}{\sqrt{1-\beta^2}}$, où $\beta$ est appelé vitesse réduite telle que $\beta=\dfrac{v}{c}$, alors :
- $x'=\gamma\;(x-vt)$, $y'=y$, $z'=z$ ;
- $t'=\gamma\left(t-\beta\,\dfrac{x}{c}\right)$.
On retrouve alors (
1. la contraction des longueurs pour la règle : $L'=\dfrac{L}{\gamma}$ ;
2. la dilatation du temps pour les miroirs : $t'=\gamma \,t$ (ce sont des temps propres $\large\tau$)
Dans l'exemple de la figure, il suffit d'utiliser le théorème de Pythagore :
- $L^2+(vt'/2)^2=(ct'/2)^2$, d'où en isolant $t'$,
- $t'=2L/\sqrt{c^2-v^2}=2L/c\cdot1/\sqrt{1-v^2/c^2}$.
- Or, $t=2L/c$ d'où $t'=\gamma \,t$.
Expériences de pensée
On dénombre plusieurs expériences de pensée (en allemand : Gedankenexperiment) qu'aimaient bien Albert Einstein pour illustrer quelques phénomènes relativistes contre-intuitifs.

(Photo-montage : vetopsy.fr)
1. Les paradoxes des vitesses sont simples et du genre 250 000 + 250 000 = 299 792 458, puisque aucune vitesse peur dépasser la vitesse de la lumière.
2. Le paradoxe de la grange démontre la contraction des longueurs.
3. Le paradoxe des jumeaux ou paradoxe des horloges (Clock paradox) a été présenté par Paul Langevin (1872-1846) au congrès de Bologne en 1911. Sa résolution divise encore (cf. les facettes du paramètre des jumeaux et 

La conclusion, généralement admise est que le jumeau voyageur finit plus jeune que celui resté sur Terre.
- Cela est dû à la dissymétrie car le jumeau voyageur change de référentiel galiléen pour revenir.
- Les durées de vie de la création à l’annihilation de muons sont considérées comme en accord avec cette conclusion.
Retour à la relativité restreinte ou aller à la relativité générale
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant Eintein Relativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


