Mécanique quantique
Champs en physiques classique et quantique
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires

Un champ est la donnée, pour chaque point de l’espace, de la valeur d’une grandeur physique (température, vitesse, charge, masse, potentiel…).
Ces champs peuvent être :
- scalaire (température, pression...),
- vectoriel (vitesse des particules d'un fluide, champ électrique...),
- spinoriel, i.e. utilisant les spineurs et en particulier les spineurs de Dirac.
(Figure : vetopsy.fr)
Cette classification repose sur les propriétés de transformations des champs sous l'action d'opérateurs associés aux groupes de symétries.

Vous pouvez lire : Qu’est-ce qu’un champ (en physique) ?
Champs
en physique classique
La physique classique ne considérait que les propriétés des objets matériels pour décrire la nature.
Dans ce cas, le champ est une autre façon de décrire les interactions fondamentales comme des " actions à distance ".
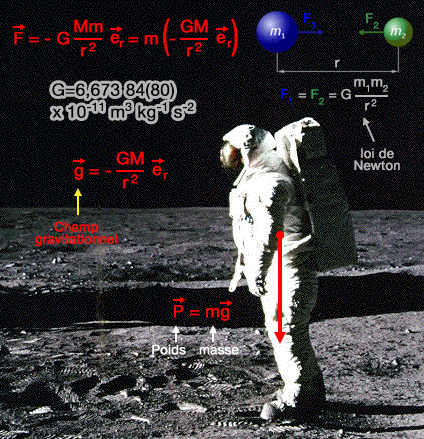
Gravitation
Dans la gravitation, la loi de gravitation universelle d'Isaac Newton (1642-1726) exprime simplement la force qui agit entre deux corps massifs. Toutefois, si on étudie plusieurs corps, la fait séparer chaque fois les calculs pour une paire de corps devient très rapidement fastidieux.
- Il fallait bien expliquer les forces qui s'exercent entre les corps, via le vide qui les sépare. Ainsi, dans une lettre de 1692 à Richard Bentley, Newton indique : « Que la gravité soit innée, inhérente et essentielle à la matière, en sorte qu'un corps puisse agir sur un autre à distance au travers du vide, sans médiation d'autre chose, par quoi et à travers quoi leur action et force puissent être communiquées de l'un à l'autre est pour moi une absurdité dont je crois qu'aucun homme, ayant la faculté de raisonner de façon compétente dans les matières philosophiques, puisse jamais se rendre coupable. »
- Cette force agit donc immédiatement quel que soit la distance entre les corps, ce qui va poser un problème par la suite à Albert Einstein dans sa relativité restreinte qu'il transforma en relativité générale.
- De nombreux scientifiques utilisèrent alors la notion d'éther pour remédier à cette difficulté.
(Figure : vetopsy.fr)
Les physiciens de cette époque considéraient l'espace comme un volume dans lesquels se déroulaient des événements évoluant dans un temps absolu et défini qui dépendaient d'objets physiques.
Au XVIIIe siècle, on définit le champ gravitationnel qui donne qui donne à chaque point de l'espace une force gravitationnelle totale ressentie par un objet avec une masse unitaire à ce point.
- Ce champ n'est alors qu'une astuce mathématique (cf. Wikipedia pour l'aspect historique).
- Mais, c'est bien la définition du champ donné plus haut.
Électrostatique
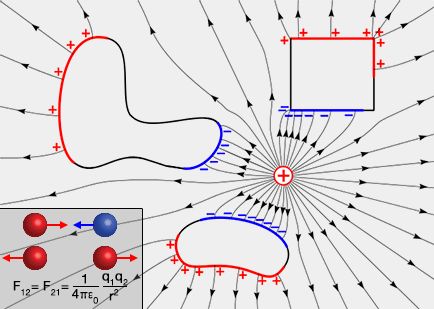
En 1785, le physicien français Charles-Augustin Coulomb (1736-1806) énonce la loi fondamentale de l'électrostatique, i.e. force d'interaction électrique entre deux particules chargées.
La force coulombienne $\vec F_{12}$ exercée par une charge électrique $q_1$ placée au point $\vec r_1$ sur une charge $q_2$ placée au point $\vec r_2$ est :
$\vec F_{12}=\dfrac{q_1q_2}{4\pi\epsilon_0}\dfrac{\vec r_2-\vec r_1}{||\vec r_2-\vec r_1||^3}$, sous forme scalaire, $\vec F_{12}=\dfrac{1}{4\pi\epsilon_0}\dfrac{|q_1q_2|}{r^2}$.

$\epsilon_0$ est la permittivité du vide, et $k_C=1/4\pi\epsilon_0$ est appelée constante de Coulomb.
Selon la charge respective des particules, on parle d'attraction ou de répulsion coulombienne.
- Cette répulsion coulombienne est représentée comme une barrière coulombienne qui doit être vaincue lors de fusion nucléaire par exemple dans la nucléosynthèse, réaction possible grâce aux températures très élevées dans les étoiles.
- Dans la radioactivité alpha (α), l'effet tunnel intervient.
On définit :
- un champ électrostatique $\vec E$, tel que $\vec F=q\vec E$,
- une énergie potentielle électrostatique.
Magnétisme
Dans la première moitié du XIXe siècle, Michael Faraday (1791-1867) utilisa le concept de champ pour décrire le champ magnétique qui ne s'exerce pas selon une seule direction comme la gravitation : il énonce la loi de Faraday qui rapproche l'électricité et magnétisme.
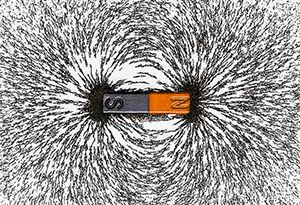
On peut " voir " les lignes de champ, i.e. lignes qui relient les points qui ont même valeur. Ces lignes de champ sont orthogonales aux équipotentielles du même champ. C'est le cas par exemple :
- des cartes de la météo qui montent les pressions atmosphériques ou la vitesse des vents,
- de la limaille de fer qui matérialise le champ électromagnétique.
Électromagnétisme
En 1864, James Clerk Maxwell (1831-1879), unifia les phénomènes électriques et magnétiques dans sa théorie de l'électromagnétisme.
Il écrit dans cet article intitulé " A Dynamical Theory of the Electromagnetic Field " : « L'accord des résultats semble montrer que la lumière et le magnétisme sont deux phénomènes de même nature et que la lumière est une perturbation électromagnétique se propageant dans l'espace suivant les lois de l'électromagnétisme. »
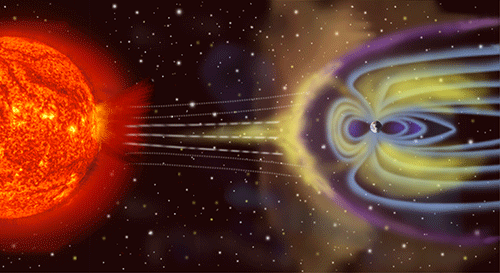
le champ magnétique terrestre (surtensions dans les réseaux électriques)
Maxwell montre donc que la lumière est une onde électromagnétique (non corpusculaire) et définit donc le champ électromagnétique.
- D'une part, les ondes dans ce champ se propagent à une vitesse finie.
- D'autre part, pour lui, elles ne peuvent pas se propager dans le vide tout comme le son. Il reprend alors la notion d'éther, appelé maintenant éther luminifère, déjà utilisée dans la gravitation.
Les lois de l'électromagnétisme prédisent que la vitesse de la lumière est indépendante de la vitesse d'un observateur par rapport à la source qui émet la lumière, ce qui est incompatible avec les lois de la mécanique classique newtonienne.
En 1931, pour le centenaire de la naissance de Maxwell, Einstein décrivit les travaux de Maxwell comme les « plus profonds et fructueux que la physique ait connu depuis le temps de Newton ».
Champs en physique quantique
La théorie des quanta, initié par Max Planck (1858-1947) en 1900, fut développée par Albert Einstein (1879-1955) en 1905 - année magique (annus mirabilis) -.

1. Dans son premier article de mars 1905, il montre que la lumière n'est composée que de quanta, appelés plus tard photons.
2. Dans son troisième article de juin, qui décrit la relativité restreinte :
- il supprime la notion d'éther, met en place les fondements de la théorie des champs pour prouver que les ondes électromagnétiques peuvent se déplacer dans le vide.
- L'espace et le temps ne sont plus absolus comme chez Newton, mais liés de manière dynamique.
- Il répond au paradoxe de Maxwell en remplaçant les lois de la mécanique classique par celles de la relativité restreinte, pour démontrer que la vitesse des ondes est identique pour tous les observateurs.

Le photon, qui provient d'un champ électromagnétique, représente une quantification de ce champ.

Entre 1907 et 1915, Albert Einstein énonça sa théorie de la relativité générale, dans laquelle l'espace-temps est considéré sous la forme d'un champ gravitationnel dynamique, à la manière du champ électromagnétique de Maxwell.
- L'espace de Newton est un champ gravitationnel.
- Des champs se propagent sur d'autres champs et, après les découvertes suivantes, l'univers ne sera plus composé que de particules et de champs.
Puis, en 1923, Louis de Broglie (1892-1987) montre que tous les objets ont une double nature d'onde et de corpuscule, bien que ce phénomène ne soit perceptible qu'à l'échelle de l'atome.
- Une des conséquences fondamentales de cette dualité est qu'il existe alors pour chaque particule un champ fondamental dont l'excitation représente la particule elle-même, comme on le fait déjà pour le photon.
- Les interactions quantiques sont des termes d’interactions entre les différents champs sous forme de perturbations.
Les champs électromagnétiques peuvent donc être considérés comme des entités physiques.
Richard Feymann (1918-1988) écrit : « The fact that the electromagnetic field can possess momentum and energy makes it very real... a particle makes a field, and a field acts on another particle, and the field has such familiar properties as energy content and momentum, just as particles can have. ».
En 1927, Paul Dirac (1902-1984) utilisa la notion de champ quantique pour expliquer l'émission spontanée des photons lors du retour de l'électron sur une couche inférieure de l'atome et, en 1928, introduisit sa fameuse équation qui introduit la relativité dans l’équation de Schrödinger.
Par la suite, toutes les particules sont considérées comme les quanta d'un champ quantique.

Ce phénomène est à la base de la théorie quantique des champs (cf. histoire et applications), utilisée dans
- l’électrodynamique quantique (QED),
- la chromodynamique quantique,
- la théorie électrofaible,
- le modèle standard des particules.
Propriétés des champs quantiques
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinte Champs en physique Mécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiquesPostulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


