Mécanique quantique
Postulats
- Mathématiques
- Mécanique quantique
- Dualité onde-corpuscule
- Relativité
- Champs en physique
- Rappels de mécanique classique newtonienne
- Rappels de mécanique analytique
- Moments en mécanique quantique
- Nombres quantiques
- Postulats de la mécanique quantique
- Postulat I : principe de superposition
- Postulat II : principe de correspondance
ou description quantique d'une grandeur physique - Postulat III : principe de quantification
ou valeurs possibles d'une observable - Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde - Postulat V : réduction du paquet d'onde
- Postulat VI : évolution temporelle de l'état quantique
- Principe d'incertitude
- Observables
- État quantique
- Fonction d'onde
- Symétries
- Modèle standard des particules
- Interactions fondamentales ou élémentaires

Cette page rappelle très succinctement les postulats de la mécanique quantique pour pouvoir se faire une idée du modèle standard des particules élémentaires.
Elle reprend les notions de la page Wikipedia en français : vous trouverez les liens sur le site pour expliciter les concepts.
Dans la mécanique quantique, qui est non-déterministe, l'état du système permet seulement de prévoir, de façon toutefois parfaitement reproductible, les probabilités respectives des différents résultats (cf. principe d'incertitude).

La vision de la mécanique quantique nous pose de nombreux problèmes qui dépassent largement notre expérience de la réalité (cf. interprétations et chat de Schrödinger).
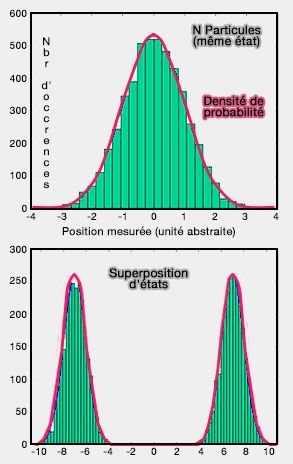
(Figure : vetopsy.fr d'après Perrin)
L'abord du sujet est complexe (c'est le cas de le dire) et les rappels seront sommaires pour les initiés.
On peut formuler mathématiquement la mécanique quantique en 6 postulats.
Les trois axiomes de la mécanique quantique est une théorie concurrente.
Postulat I : principe de superposition
Un état quantique peut être représenté, à chaque instant t, par un vecteur dans un espace de Hilbert $\mathcal H$.
- Il est habituellement noté sous la forme d'un ket $|\psi (t)\rangle$.
- Si on veut être précis, ce sont des vecteurs normalisés à une phase près $\big(|\psi\rangle\sim|\psi\rangle e^{i\alpha}\big)$.
La superposition des états en est la conséquence directe :
- le spin, par exemple, est calculé (en notation bra-ket) par : $\vert\psi\rangle=\dfrac {1}{\sqrt 2}\bigg(\vert\uparrow\downarrow\rangle-|\downarrow\uparrow\rangle\bigg)$ qui implique la superposition des états de spin communs pour deux particules de spin 1/2 (fermions)
- Dans les espaces hilbertiens, toute combinaison linéaire fait partie de l'espace des états : si $|\psi _1\rangle$ et $|\psi _2\rangle$ décrivent deux états du système et si $\lambda$ est un complexe, alors la combinaison linéaire $\lambda|\psi_1\rangle+|\psi _2\rangle$ décrit un état du système.
Postulat II : principe de correspondance
ou description quantique d'une grandeur physique
À toute propriété observable, appelé observable tout court, $A$, (position, quantité de mouvement, spin, impulsion/énergie…), correspond un opérateur hermitien dit linéaire, $\hat A$, agissant sur les vecteurs d'un espace de Hilbert $\mathcal H$.
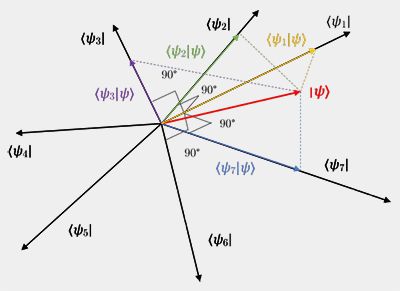
(Figure : physicsandchemistryrevision.tumblr.com)
Les observables $A$ sont des opérateurs auto-adjoints sur $\mathcal H$, $A=A^\dagger$. Les quantités observables sont les $\langle\psi|A|\phi\rangle$.
Ces observables sont :
- l'opérateur de position : $\hat Q=r$ ;
- l'opérateur d'énergie potentielle classique ou électromagnétique : $\hat V(r)=V_{cl}(r)$ ;
- l'opérateur de quantité de mouvement : $\hat P(r)=-i\hbar\nabla$ ou $\nabla$ st l'opérateur laplacien qui transforme la position $r$.
- l'opérateur de moment angulaire : $\hat L(r)=\hat Q\times\hat P=-i\hbar r\times\nabla$ ;
- l'opérateur d'énergie cinétique : $\hat K(r)=\dfrac{\hat P\cdot\hat P}{2m}=-\dfrac{\hbar ^2}{2m}\nabla ^2$ ;
- l'opérateur d'énergie totale (hamiltonien) : $\hat H=\hat K+\hat V=\hat K(r)+V_{cl}(r)$ ;
- l'opérateur action du système, appelé lagrangien : $\hat L=\hat K-\hat V$.
Postulat III : principe de quantification ou valeurs possibles d'une observable

il ne change pas la direction. La valeur propre est 1.
(Figure : vetopsy.fr d'après TreyGreer62)
La mesure de l'observable $A$ ne peut fournir que l'une des valeurs propres de $A$ : ces valeurs propres sont réelles.
- Les valeurs propres sont les valeurs pouvant résulter d'une mesure idéale de cette observable.
- Les vecteurs propres étant l'état quantique du système immédiatement après la mesure et résultant de cette mesure (cf. postulat V).
$\hat A|\alpha _n\rangle=a_n|\alpha_n\rangle$ où $\hat A$ est l'observable, $|\alpha_n\rangle$, le vecteur propre et $\alpha_n$ la valeur propre correspondante.$\ell $
Les états propres de tout observable $\hat A$ sont complets et forment une base de Hilbert (orthonormée) dans l'espace de Hilbert : tout vecteur $|\psi (t)\rangle$ peut se décomposer de manière unique sur la base de ces vecteurs propres $|\phi_i\rangle$, tel que :
$|\phi\rangle=c_1|\phi_1+c_2|\phi_2+...+c_n|\phi_n+...$
Postulat IV : décomposition spectrale ou
interprétation probabiliste de la fonction d'onde
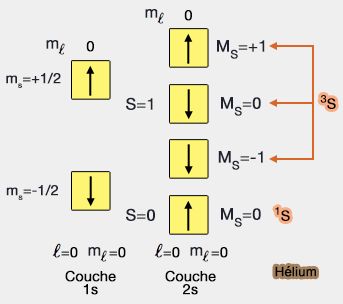
(Figure : vetopsy.fr)
La mesure d'une grandeur physique représentée par l'observable $A$, effectuée sur l'état quantique normalisé $|\psi (t)\rangle$, donne comme résultat la valeur propre $a_n$, avec la probabilité $P(a_n).
1. Cas d'un spectre discret non dégénéré : $P(a_n)=|\langle u_n|\psi\rangle|^2$, où $|u_n\rangle $ est le vecteur propre normé de $A$ associé à la valeur propre $a_n$.
2. Cas d'un spectre discret dégénéré : $P(a_n)=\sum\limits_{i}|\langle u_n^i|\psi\rangle|^2$, où $i= 1,2... g_n$ ($g_n$ étant le degré de dégénérescence de $a_n$) et $|u^i_n\rangle$ un système orthonormé de vecteurs formant une base dans le sous-espace propre $E_n$ associé à la valeur propre $a_n$ de l'observable $A$.
Dans le cas d'un spectre continu et non-dégénéré, la probablité $dP(a)$ pour obtenir un résultat entre $a$ et $a+da$ est : $dP(a)=|\langle\nu_a|\psi\rangle|^2da$, où $|\nu_a\rangle$ est le vecteur propre associé à la valeur propre $a$ de l'observble $A$.
Postulat V : réduction du paquet d'onde
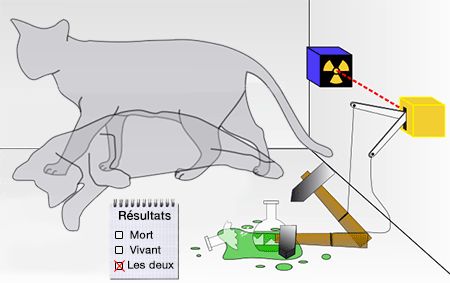
(Figure : vetopsy.fr d'après Dhatfield)
La réduction du paquet d'onde est un concept de la mécanique quantique selon lequel, après une mesure, un système physique voit son état entièrement réduit à celui qui a été mesuré (cf. principe d'incertitude).
Si la mesure de la grandeur physique $A$, à l'instant $t$, sur un système représenté par le vecteur $|\psi (t)\rangle$ donne comme résultat la valeur propre $a_n$, alors l'état du système immédiatement après la mesure est projeté sur le sous-espace propre associé à $a_n$ :
$$|\psi (t)\rangle=\dfrac{\hat P_n|\psi\rangle}{\sqrt {P(a_n)}}$$
où $P(a_n)$ est la probabilité de trouver comme résultat la valeur propre $a_n$ et $\hat P_n$ est l'opérateur projecteur défini par : $\hat P_n=\sum\limits_{k=1}^{g_n}|u_{n,k}\rangle\langle u_{n,k}|$ avec $g_n$, le degré de dégénérescence de la valeur propre $a_n$ et les $|u_{n,k}\rangle$ les vecteurs de son sous-espace propre.
Postulat VI : évolution temporelle de l'état quantique
L'état $|\Psi,t\rangle$ de tout système quantique non-relativiste est une solution de l'équation de Schrödinger dépendante du temps qui est la généralisation de l'équation de l'énergie totale de Louis de Broglie : $E_{totale}=\dfrac{p^2}{2m}+V(t)$.
$$i\hbar\dfrac{\partial}{\partial_t}|\Psi(t)\rangle=\hat H|\Psi(t)\rangle$$
- dans laquelle, $i$ est l'unité imaginaire ($i^2=−1$) ;
- $\hbar$ est la constante de Planck réduite ou de Dirac ($\hbar=h/2\pi$) ;
- $\hat H=\dfrac{\hat{\vec P}^2}{2m}+V(\hat{\vec r},t)$ est l'hamiltonien, dépendant du temps en général, l'observable correspondant à l'énergie totale du système, c'est-à-dire la somme de l'énergie cinétique et l'énergie potentielle ;
- $\hat{\vec P}$ est l'observable impulsion ;
- $\hat{\vec r}$ est l'observable position.

L'équation de Schrödinger est l'équation dynamique de la mécanique quantique.
La généralisation de l'équation de Schrödinger au domaine relativiste aboutira à l'équation de Dirac qui établit l'existence du spin et des antiparticules.
Principe d'incertitude
MathématiquesMécanique quantiqueDualité onde-corpusculeRelativité avant EinteinRelativité restreinteChamps en physiqueMécanique newtonienneMécanique analytiqueMoments en mécanique quantiqueMoments angulairesMoments magnétiquesNombres quantiques Postulats de la mécanique quantiquePrincipe d'incertitudeObservablesÉtat quantiqueFonction d'ondeÉquation de SchrödingerOrbitalesÉquation de DiracSpin-orbitalesCouplage spin-orbiteConfiguration électroniqueSymétriesGroupes de symétrieParité ou symétrie $\mathcal P$ Hélicité et chiralitéSymétries $\mathcal C$, $\mathcal C\mathcal P$, $\mathcal C\mathcal P$, $\mathcal T$, $\mathcal C\mathcal P\mathcal T$Modèle standard des particules


